
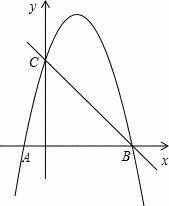
如图,抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,与x轴交于另一点B.
(1)求抛物线的解析式;
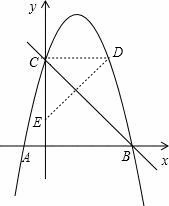
(2)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标.
考点: 待定系数法求二次函数解析式;二次函数图象上点的坐标特征;坐标与图形变化-对称.
专题: 压轴题.
分析: (1)由于抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,利用待定系数法即可确定抛物线的解析式;
(2)由于点D(m,m+1)在第一象限的抛物线上,把D的坐标代入(1)中的解析式即可求出m,然后利用对称就可以求出关于直线BC对称的点的坐标.
解答: 解:(1)∵抛物线y=ax2+bx﹣4a经过A(﹣1,0)、C(0,4)两点,
∴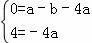 ,
,
解之得:a=﹣1,b=3,
∴y=﹣x2+3x+4;
(2)∵点D(m,m+1)在第一象限的抛物线上,
∴把D的坐标代入(1)中的解析式得
m+1=﹣m2+3m+4,
∴m=3或m=﹣1,
∴m=3,
∴D(3,4),
∵y=﹣x2+3x+4=0,x=﹣1或x=4,
∴B(4,0),
∴OB=OC,
∴△OBC是等腰直角三角形,
∴∠CBA=45°
设点D关于直线BC的对称点为点E
∵C(0,4)
∴CD∥AB,且CD=3
∴∠ECB=∠DCB=45°
∴E点在y轴上,且CE=CD=3
∴OE=1
∴E(0,1)
即点D关于直线BC对称的点的坐标为(0,1);
点评: 此题考查传统的待定系数求函数解析式,第二问考查点的对称问题,作合适的辅助线,根据垂直和三角形全等来求P点坐标


科目:初中数学 来源: 题型:
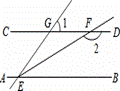
如图,已知直线AB∥CD,∠GEB的平分线EF交C D于点F,∠1=60°,则∠2等于( )
A.130° B.140° C.150° D.160°
查看答案和解析>>
科目:初中数学 来源: 题型:
某公司在工程招标时,接到甲、乙两个工程队的投标书.每施工一天,需付甲工程队工程款1.5万元,付乙工程队工程款1.1万元,工程领导小组根据甲、乙两队的投标书测算,形成下列三种施工方案:
①甲队单独完成此项工程刚好如期完工;②乙队单独完成此项工程要比规定工期多用5天;③若甲、乙两队合作4天,剩下的工程由乙队独做也正好如期完工;
如果工程不能按预定时间完工,公司每天将损失3000元,你觉得哪一种施工方案最节省工程款,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com