
分析 根据[x]表示不超过x的最大整数可知,3[x]为整数,则17{x}为整数;无论x是正数还是负数,x-[x]必然为非负数,2012除以3余数为2,则17{x}除以3的余数是1,可求出17{x}的取值为1、4、7、10、13、16,代入3[x]-17{x}=2012即可求出17{x}的取值,从而求出{x}的值,再代入3[x]-17{x}=2012即可求出[x],利用x=[x]+{x}即可求出x的值,相加即可.
解答 解:∵17{x}必为整数,且除以3的余数是1,同时0≤17{x}<17;
∴17{x}的取值为1、4、7、10、13、16,
即:{x}为$\frac{1}{17}$、$\frac{4}{17}$、$\frac{7}{17}$、$\frac{10}{17}$、$\frac{13}{17}$、$\frac{16}{17}$;
相应地,[x]依次为:671、670、669、668、667、666;
∴x=[x]+{x};
∴满足条件的x的和为(671+666)×3+3=4014.
故答案为4014.
点评 本题考查了取整计算,根据题意弄清取整的意义,结合除法运算,利用余数即可解答.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
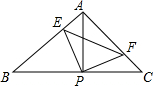 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③2S四边形AEPF=S△ABC;④BE+CF=EF.上述结论中始终正确的有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小强想知道广场上旗杆的高度,他发现旗杆顶端的绳子垂到旗台上还多0.8米,当他把绳子的下端在旗台上拉开2米后,发现下端刚好接触旗台面,你能帮他算出来这根旗杆的高吗?
小强想知道广场上旗杆的高度,他发现旗杆顶端的绳子垂到旗台上还多0.8米,当他把绳子的下端在旗台上拉开2米后,发现下端刚好接触旗台面,你能帮他算出来这根旗杆的高吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com