

分析 设x张用A方法,y张用B方法,就可以分别表示出侧面个数和底面个数;再由侧面个数和底面个数比为3:2建立方程组,求出侧面的总数就可以求出结论.
解答 解:设裁剪时x张用A方法,y张用B方法.
由题意,得$\left\{\begin{array}{l}{x+y=19}\\{\frac{6x+4y}{5y}=\frac{3}{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=7}\\{y=12}\end{array}\right.$,
∴盒子的个数为:$\frac{6×7+4×12}{3}$=30.
答:裁剪时7张用A方法,12张用B方法,裁剪出的侧面和底面恰好全部用完,能做30个盒子.
点评 本题考查了二元一次方程组的应用,解答时根据裁剪出的侧面和底面个数相等建立方程组是关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
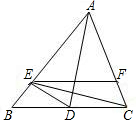 如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是①②③(填序号).
如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②CE平分∠DEF;③AD垂直平分CE.其中正确的是①②③(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|+$\sqrt{m+n-18}$=0.
已知线段AB=m,CD=n,线段CD在直线AB上运动(A在B左侧,C在D左侧),若|m-2n|+$\sqrt{m+n-18}$=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
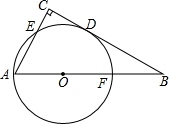 如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com