
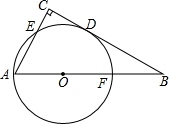
 如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
如图,在△ABC中,∠C=90°,以AB上的一点O为圆心.OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.分析 (1)作OH⊥AC于H,连结OD,如图1,设⊙0的半径为r,根据切线的性质得OD⊥BC,则可证明四边形ODCH为矩形,得到OH=CD=6,CH=OD=r,则AH=AC-CH=10-r,然后在Rt△OAH中利于勾股定理得(10-r)2+62=r2,再解方程即可;
(2)连结OD,如图2,由平行四边形的性质得到EF∥BD,ED∥BF,利于OD⊥BD得到OD⊥EF,根据垂径定理得OD平分EF,即OD垂直平分EF,再证明∠DEF=∠OEF,由于EF⊥OD,所以EF平分OD,则OD与EF互相垂直平分,然后根据菱形的判定方法可判断四边形0FDE为菱形.
解答 解:(1)作OH⊥AC于H,连结OD,如图1,设⊙0的半径为r,
∵BC为⊙O的切线,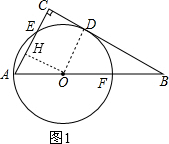
∴OD⊥BC,
∵∠C=90°,OH⊥AC,
∴四边形ODCH为矩形,
∴OH=CD=6,CH=OD=r,
∴AH=AC-CH=10-r,
在Rt△OAH中,∵AH2+OH2=OA2,
∴(10-r)2+62=r2,解得r=$\frac{34}{5}$;,
即⊙0的半径为$\frac{34}{5}$;
(2)四边形0FDE为菱形.理由如下:
连结OD,如图2,
∵四边形BDEF是平行四边形,
∴EF∥BD,ED∥BF,
∵OD⊥BD,
∴OD⊥EF,
∴OD平分EF,即OD垂直平分EF,
∵ED∥OF,
∴∠DEF=∠OFE,
而∠OFE=∠OEF,
∴∠DEF=∠OEF,
而EF⊥OD,
∴EF平分OD,
∴OD与EF互相垂直平分,
∴四边形0FDE为菱形.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了勾股定理和菱形的判定.


科目:初中数学 来源: 题型:选择题
| A. | ax2=bx | B. | x2+3y-1=0 | C. | 3x2-2x+$\frac{1}{x}$=0 | D. | 2(x+1)(x-1)=x+5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
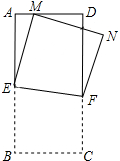 如图,在长方形纸片ABCD中,AB=mAD,其中m≥1,将它沿EF折叠(点E、F分在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,若∠BEF=α,$\frac{AM}{EF}$的值(用含m,α的式子表示).
如图,在长方形纸片ABCD中,AB=mAD,其中m≥1,将它沿EF折叠(点E、F分在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,若∠BEF=α,$\frac{AM}{EF}$的值(用含m,α的式子表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小强想知道广场上旗杆的高度,他发现旗杆顶端的绳子垂到旗台上还多0.8米,当他把绳子的下端在旗台上拉开2米后,发现下端刚好接触旗台面,你能帮他算出来这根旗杆的高吗?
小强想知道广场上旗杆的高度,他发现旗杆顶端的绳子垂到旗台上还多0.8米,当他把绳子的下端在旗台上拉开2米后,发现下端刚好接触旗台面,你能帮他算出来这根旗杆的高吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com