【题目】一套数学题集共有100道题，甲、乙和丙三人分别作答，每道题至少有一人解对，且每人都解对了其中的60道．如果将其中只有1人解对的题称作难题，2人解对的题称作中档题，3人都解对的题称作容易题，那么下列判断一定正确的是（ ）
A.容易题和中档题共60道B.难题比容易题多20道
C.难题比中档题多10道D.中档题比容易题多15道
应用题作业本系列答案科目：初中数学 来源： 题型：
【题目】问题提出
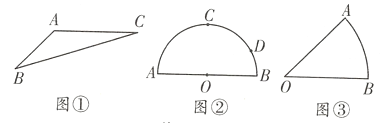
（1）如图①，在
中，
，求的面积．
问题探究
（2）如图②，半圆
的直径
，
是半圆
的中点，点
在
上，且
，点
是
上的动点，试求
的最小值．
问题解决
（3）如图③，扇形
的半径为
在选点，在边
上选点
，在边
上选点
，求
的长度的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
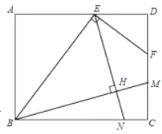
【题目】如图，矩形
中，点E在
上，过点E作
交
于F，且
，
，点M是线段
上的动点，连接
，过点E作的垂线交
于点N，垂足为H．以下结论：①
；②
；③
；④连接
，则的最小值为
；其中正确的结论是____________（所有正确结论的序号都填上）．
查看答案和解析>>
科目：初中数学 来源： 题型：
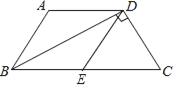
【题目】已知：如图，四边形ABCD中，AD∥BC，对角线BD平分∠ABC，且BD⊥DC，E为BC中点，AB＝DE．
（1）求证：四边形ABED是菱形；
（2）若∠C＝60°，CD＝4，求四边形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
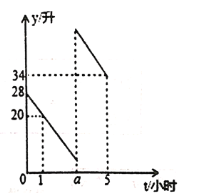
【题目】李师傅驾车从甲地到乙地，途中在加油站加了一次油，加油时，车载电脑显示油箱中剩余油量4升，已知汽车行驶时，每小时耗油量一定，设油箱中剩余油量为
（升），汽车行驶时间为
（时）,与之间的函数图像如图所示．
（1）求李师傅加油前与之间的函数关系式；
（2）求
的值；
（3）李师傅在加油站的加油量．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】电器专营店的经营利润受地理位置、顾客消费能力等因素的影响，某品牌电脑专营店设有甲、乙两家分店，均销售A、B、C、D四种款式的电脑，每种款式电脑的利润如表1所示．现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式，统计各种款式电脑的销售数量，如表2所示．
表1：四种款式电脑的利润
电脑款式 | A | B | C | D |
利润（元/台） | 160 | 200 | 240 | 320 |
表2：甲、乙两店电脑销售情况
电脑款式 | A | B | C | D |
甲店销售数量（台） | 20 | 15 | 10 | 5 |
乙店销售数量（台）8 | 8 | 10 | 14 | 18 |
试运用统计与概率知识，解决下列问题：
（1）从甲店每月售出的电脑中随机抽取一台，其利润不少于240元的概率为 ；
（2）经市场调查发现，甲、乙两店每月电脑的总销量相当．现由于资金限制，需对其中一家分店作出暂停营业的决定，若从每台电脑的平均利润的角度考虑，你认为应对哪家分店作出暂停营业的决定？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
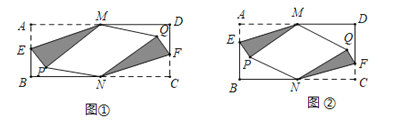
【题目】综合与实践：折纸中的数学
问题情境：
在矩形
中，
＝12，点
、
分别是、
的中点，点
、
分别在
、
上，且
＝
，将△
沿
折叠，点
的对应点为点
，将△
沿
折叠，点
的对应点为点Q，且点、
均落在矩形的内部（如图①）．
数学思考：
（1）判断
与
是否平行，并说明理由；
（2）当长度是多少时，存在点，使四边形
是有一个内角为60°的菱形（如图②）？直接写出的长度及菱形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
，
，直线
．
（1）若该抛物线与
轴交点的纵坐标为
，求该抛物线的顶点坐标；
（2）证明：该抛物线与直线
必有两个交点；
（3）若该抛物线经过点
，且对任意实数
，不等式
都成立；当
时，该二次函数的最小值为
．求直线
的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数
的图象与y轴交于C点，交x轴于点A（-2，0），B（6，0），P是该函数在第一象限内图象上的动点，过点P作PQ⊥BC于点Q，连接PC，AC．
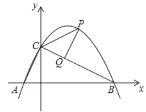
（1）求该二次函数的表达式；
（2）求线段PQ的最大值；
（3）是否存在点P，使得以点P，C，Q为顶点的三角形与△ACO相似？若存在，请求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
