
【题目】综合与实践:折纸中的数学
问题情境:
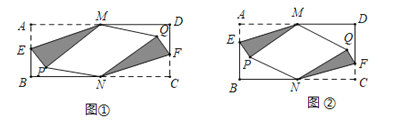
在矩形![]() 中,
中,![]() =12,点
=12,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() =
=![]() ,将△
,将△![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点
的对应点为点![]() ,将△
,将△![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点Q,且点
的对应点为点Q,且点![]() 、
、![]() 均落在矩形
均落在矩形![]() 的内部(如图①).
的内部(如图①).
数学思考:
(1)判断![]() 与
与![]() 是否平行,并说明理由;
是否平行,并说明理由;
(2)当![]() 长度是多少时,存在点
长度是多少时,存在点![]() ,使四边形
,使四边形![]() 是有一个内角为60°的菱形(如图②)?直接写出
是有一个内角为60°的菱形(如图②)?直接写出![]() 的长度及菱形
的长度及菱形![]() 的面积.
的面积.
【答案】(1)平行,证明见解析;(2)AB= =6,菱形![]() 的面积=
的面积=![]()
【解析】
(1)延长NQ交AD的延长线于H.首先证明△EAM≌△FCN,进一步得出∠AMP=∠QNC,从而可证明∠AMP=∠AHN,由此得出结论;
(2)由折叠得到PM=6,由直角三角形的性质得AO、PO的长,再根据菱形的性质得PQ,MN的长,从而解决问题.
如图中,延长NQ交AD的延长线于H.

∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,∠A=∠C=90°,
∵点M,N分别是AD,BC的中点,
∴AM=NC,
∴PM=NQ,
∵AE=CF,
∴△EAM≌△FCN(SAS),
∴∠AME=∠CNF,
∵∠AME=∠EMP,∠CNF=∠FNQ,
∴∠AMP=∠QNC,
∵AD∥BC,
∴∠AHN=∠CNH,
∴∠AMP=∠AHN,
∴PM∥NH,即PM//NQ;
(2) 连接MN、PQ相交于点O,如图,

∵四边形ABCD是矩形,AD=12,点M是AD的中点,
∴AM=6,
由折叠得,PM=AM=6,
∵四边形PNQM是菱形,且∠MPN=60°,
∴∠MPO=30°,MN⊥PQ
∴MO=3,PO=![]()
∴AB=MN=2MO=6,PQ=2PO=6![]()
∴菱形![]() 的面积=
的面积=![]() .
.


科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
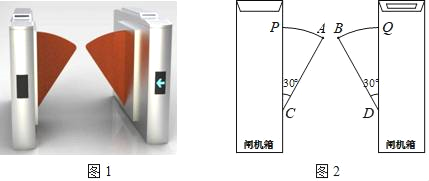
A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B位于A南偏西37°方向, 港口C位于A南偏东35°方向,B位于C正西方向. 轮船甲从A出发沿正南方向行驶40海里到达点D处,此时轮船乙从B出发沿正东方向行驶20海里至E处,E位于D南偏西45°方向.这时,E处距离港口C有多远? (参考数据:tan37°≈0.75,tan35°≈0.70)
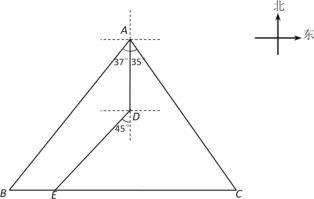
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一套数学题集共有100道题,甲、乙和丙三人分别作答,每道题至少有一人解对,且每人都解对了其中的60道.如果将其中只有1人解对的题称作难题,2人解对的题称作中档题,3人都解对的题称作容易题,那么下列判断一定正确的是( )
A.容易题和中档题共60道B.难题比容易题多20道
C.难题比中档题多10道D.中档题比容易题多15道
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的顶点
的顶点![]() 是直线
是直线![]() 和直线
和直线![]() 的交点.
的交点.
(1)用含![]() 的代数式表示顶点
的代数式表示顶点![]() 的坐标.
的坐标.
(2)①当![]() 时,
时,![]() 的值均随
的值均随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
②若![]() ,且
,且![]() 满足
满足![]() 时,二次函数的最小值为
时,二次函数的最小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)试证明:无论![]() 取任何值,二次函数
取任何值,二次函数![]() 的图象与直线
的图象与直线![]() 总有两个不同的交点.
总有两个不同的交点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③△POF∽△BNF;④当△PMN∽△AMP时,点P是AB的中点,其中一定正确的结论有_____.(填上所有正确的序号).
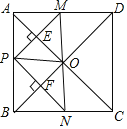
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l与反比例函数y=![]() (k≠0)的图象在第二象限交于B、C两点,与x轴交于点A,连接OC,∠ACO的角平分线交x轴于点D.若AB:BC:CO=1:2:2,△COD的面积为6,则k的值为______.
(k≠0)的图象在第二象限交于B、C两点,与x轴交于点A,连接OC,∠ACO的角平分线交x轴于点D.若AB:BC:CO=1:2:2,△COD的面积为6,则k的值为______.
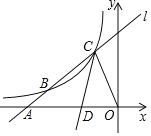
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com