
【题目】如图,B位于A南偏西37°方向, 港口C位于A南偏东35°方向,B位于C正西方向. 轮船甲从A出发沿正南方向行驶40海里到达点D处,此时轮船乙从B出发沿正东方向行驶20海里至E处,E位于D南偏西45°方向.这时,E处距离港口C有多远? (参考数据:tan37°≈0.75,tan35°≈0.70)
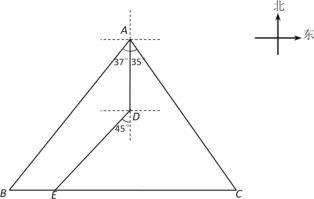
【答案】E处距离港口C约96海里
【解析】
延长AD交BC于点F,设EF=x海里,得DF=x海里,解Rt△ABF得EF=40海里,AF=80海里,再解Rt△AFC得CF=56海里,从而可得EC=96海里.
如图,延长AD交BC于点F,AF⊥BC .
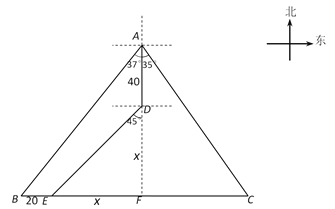
设EF=x海里.
在Rt△DEF中,∠DFE=90°,
∵tan∠EDF=![]() ,
,
∴tan45°=![]() ,
,
∴ DF=x,
在Rt△ABF中,∠DFE=90°,
∵tan∠BAF=![]() ,
,
∴BF=AF tan37°,
∴20+x≈0.75(40+x),
∴x=40,
∴AF=AD+DF=80.
在Rt△AFC中,∠AFC=90°,
∵tan∠CAF=![]() ,
,
∵tan35°=![]() ,
,
∴CF=AFtan35°≈80×0.70=56
∴CE=EF+CF=40+56=96
答:E处距离港口C约96海里.


科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本);并求出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
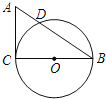
【题目】如图,在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
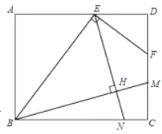
【题目】如图,矩形![]() 中,点E在
中,点E在![]() 上,过点E作
上,过点E作![]() 交
交![]() 于F,且
于F,且![]() ,
,![]() ,点M是线段
,点M是线段![]() 上的动点,连接
上的动点,连接![]() ,过点E作
,过点E作![]() 的垂线交
的垂线交![]() 于点N,垂足为H.以下结论:①
于点N,垂足为H.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④连接
;④连接![]() ,则
,则![]() 的最小值为
的最小值为![]() ;其中正确的结论是____________(所有正确结论的序号都填上).
;其中正确的结论是____________(所有正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
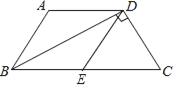
【题目】已知:如图,四边形ABCD中,AD∥BC,对角线BD平分∠ABC,且BD⊥DC,E为BC中点,AB=DE.
(1)求证:四边形ABED是菱形;
(2)若∠C=60°,CD=4,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
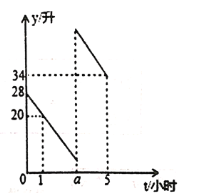
【题目】李师傅驾车从甲地到乙地,途中在加油站加了一次油,加油时,车载电脑显示油箱中剩余油量4升,已知汽车行驶时,每小时耗油量一定,设油箱中剩余油量为![]() (升),汽车行驶时间为
(升),汽车行驶时间为![]() (时),
(时),![]() 与
与![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
(1)求李师傅加油前![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求![]() 的值;
的值;
(3)李师傅在加油站的加油量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:折纸中的数学
问题情境:
在矩形![]() 中,
中,![]() =12,点
=12,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() =
=![]() ,将△
,将△![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点
的对应点为点![]() ,将△
,将△![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点Q,且点
的对应点为点Q,且点![]() 、
、![]() 均落在矩形
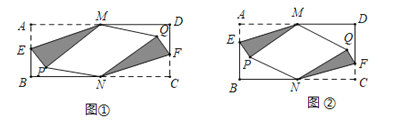
均落在矩形![]() 的内部(如图①).
的内部(如图①).
数学思考:
(1)判断![]() 与
与![]() 是否平行,并说明理由;
是否平行,并说明理由;
(2)当![]() 长度是多少时,存在点
长度是多少时,存在点![]() ,使四边形
,使四边形![]() 是有一个内角为60°的菱形(如图②)?直接写出
是有一个内角为60°的菱形(如图②)?直接写出![]() 的长度及菱形
的长度及菱形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com