
【题目】二次函数![]() 的顶点
的顶点![]() 是直线
是直线![]() 和直线
和直线![]() 的交点.
的交点.
(1)用含![]() 的代数式表示顶点
的代数式表示顶点![]() 的坐标.
的坐标.
(2)①当![]() 时,
时,![]() 的值均随
的值均随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
②若![]() ,且
,且![]() 满足
满足![]() 时,二次函数的最小值为
时,二次函数的最小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)试证明:无论![]() 取任何值,二次函数
取任何值,二次函数![]() 的图象与直线
的图象与直线![]() 总有两个不同的交点.
总有两个不同的交点.
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
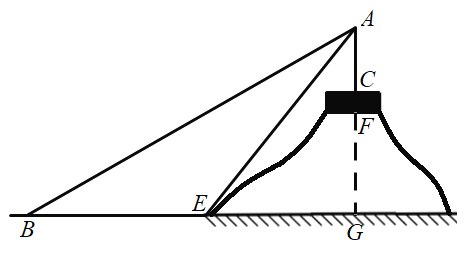
【题目】2018央视中秋晚会在曲阜尼山举行,让全国乃至全世界的目光再一次聚焦曲阜.其中世界最大最高的孔子像,位于晚会场地对面尼山圣境儒宫西侧小山上.来观看晚会的小明想测量一下远处孔子像的高度.如图,小明在B处测得孔子像的顶端A的仰角为![]() ,然后沿着正对孔子像的方向前进了160m到达E处,再次测得孔子像的顶端A的仰角
,然后沿着正对孔子像的方向前进了160m到达E处,再次测得孔子像的顶端A的仰角![]() .已知塑像的底座
.已知塑像的底座![]() ,小山的高度
,小山的高度![]() ,那么孔子像
,那么孔子像![]() 的高度是多少?(参考数据:
的高度是多少?(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
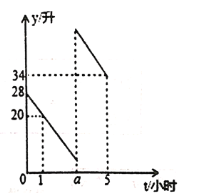
【题目】李师傅驾车从甲地到乙地,途中在加油站加了一次油,加油时,车载电脑显示油箱中剩余油量4升,已知汽车行驶时,每小时耗油量一定,设油箱中剩余油量为![]() (升),汽车行驶时间为
(升),汽车行驶时间为![]() (时),
(时),![]() 与
与![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
(1)求李师傅加油前![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)求![]() 的值;
的值;
(3)李师傅在加油站的加油量.
查看答案和解析>>
科目:初中数学 来源: 题型:
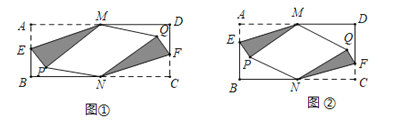
【题目】综合与实践:折纸中的数学
问题情境:
在矩形![]() 中,
中,![]() =12,点
=12,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() =
=![]() ,将△
,将△![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点
的对应点为点![]() ,将△
,将△![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点Q,且点
的对应点为点Q,且点![]() 、
、![]() 均落在矩形
均落在矩形![]() 的内部(如图①).
的内部(如图①).
数学思考:
(1)判断![]() 与
与![]() 是否平行,并说明理由;
是否平行,并说明理由;
(2)当![]() 长度是多少时,存在点
长度是多少时,存在点![]() ,使四边形
,使四边形![]() 是有一个内角为60°的菱形(如图②)?直接写出
是有一个内角为60°的菱形(如图②)?直接写出![]() 的长度及菱形
的长度及菱形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为2000元、1700元的A、B两种型号的空调,如表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
(进价、售价均保持不变,利润=销售总收入进货成本)
(1)求A、B两种型号的空调的销售单价;
(2)若超市准备用不多于54000元的金额再采购这两种型号的空调共30台,求A种型号的空调最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.

(1)如图1,取点M(1,0),则点M到直线l:y=![]() x﹣1的距离为多少?
x﹣1的距离为多少?
(2)如图2,点P是反比例函数y=![]() 在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=
在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0,问是否存在点P,使d0=![]() ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com