
����Ŀ����ͼ����O��ֱ��AB��26��P��AB��(�����A��B�غ�)����һ�㣬��C��DΪ��O�ϵ����㣬����APD����BPC����ơ�CPDΪֱ��AB�ġ������ǡ���
(1)����BPC����DPC��60�㣬���CPD��ֱ��AB�ġ������ǡ��𣿲�˵�����ɣ�
(2)��![]() �ij�Ϊ
�ij�Ϊ![]() ���������ǡ���CPD�Ķ�����
���������ǡ���CPD�Ķ�����
(3)��ֱ��AB�ġ������ǡ�Ϊ120�㣬�ҡ�PCD���ܳ�Ϊ24+13![]() ��ֱ��д��AP�ij���
��ֱ��д��AP�ij���

���𰸡�(1)��CPD��ֱ��AB�ġ������ǡ������ɼ�������(2)�������ǡ���CPD�Ķ���Ϊ45�㣻(3)����������AP�ij�Ϊ3��23��
��������
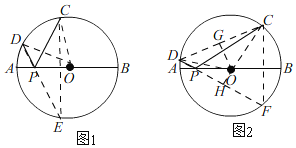
��1���ɡ�CPD����BPC�õ���APD���õ���BPC����APD�����ԡ�CPD��ֱ��AB����������������2������CD������ʽ�����COD��45������CE��AB����O��E������PE�����á�CPDΪֱ��AB���������������õ���APD����BPC����OPE����APD���õ���OPE+��CPD+��BPC��180��������D��P��E���㹲�ߣ���CED��![]() ��COD��22.5����
��COD��22.5����
�õ���OPE��90����22.5����67.5�������APD����BPC��67.5�������ԡ�CPD��45������3���ֳ����P��OA�ϻ���OB�ϵ��������OA��ʱ��ͬ����2���ķ����õ���D��P��F��ͬһ��ֱ���ϣ��õ���PCF�ǵȱ������Σ�����OC��OD������O��OG��CD��G��
����sin��DOG�����CD�������ܳ����DF����O��OH��DF��H�����ù��ɶ������OP�������õ�AP����OB��ʱ��ͬ��OA���㷽������
��CPD��ֱ��AB��������������
���ɣ��ߡ�CPD����BPC��60����
���APD��180������CPD����BPC��180����60����60����60����
���BPC����APD��
���CPD��ֱ��AB��������������
(2)��ͼ1����AB��26��
��OC��OD��OA��13��
���COD��n����
��![]() �ij�Ϊ
�ij�Ϊ![]() ����
����
��![]()
��n��45��
���COD��45����
��CE��AB����O��E������PE��
���BPC����OPE��
�ߡ�CPDΪֱ��AB��������������
���APD����BPC��
���OPE����APD��
�ߡ�APD+��CPD+��BPC��180����
���OPE+��CPD+��BPC��180����
���D��P��E���㹲�ߣ�
���CED��![]() ��COD��22.5����
��COD��22.5����
���OPE��90����22.5����67.5����
���APD����BPC��67.5����
���CPD��45����
����������������CPD�Ķ���Ϊ45����
(3)�ٵ���P�ڰ뾶OA��ʱ����ͼ2������C��CF��AB����O��F������PF��
��PF��PC��
ͬ(2)�ķ����ã���D��P��F��ͬһ��ֱ���ϣ�
��ֱ��AB������������Ϊ120����
���APD����BPC��30����
���CPF��60����
���PCF�ǵȱ������Σ�
���CFD��60����
����OC��OD��
���COD��120����
����O��OG��CD��G��
��CD��2DG����DOG��![]() ��COD��60����
��COD��60����
��DG��ODsin��DOG��13��sin60����![]()
��CD��![]() ��
��
�ߡ�PCD���ܳ�Ϊ24+13![]() ��
��
��PD+PC��24��
��PC��PF��
��PD+PF��DF��24��
��O��OH��DF��H��
��DH��![]() DF��12��
DF��12��
��Rt��OHD��OH��![]()
��Rt��OHP����OPH��30����
��OP��10��
��AP��OA��OP��3��
�ڵ���P�ڰ뾶OB��ʱ��
ͬ�ٵķ����ã�BP��3��
��AP��AB��BP��23��
��������������AP�ij�Ϊ3��23��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƿ���������![]() ��ͼ��
��ͼ��![]() ��
��![]() �ֱ���ͼ�����֧�ϣ���
�ֱ���ͼ�����֧�ϣ���![]() Ϊ�Խ���������
Ϊ�Խ���������![]() ��
��![]() �ᣮ
�ᣮ
��1�����߶�![]() ��ԭ��ʱ���ֱ�д��
��ԭ��ʱ���ֱ�д��![]() ��
��![]() ��
��![]() ��
��![]() ��һ��������ϵʽ��
��һ��������ϵʽ��
��2����![]() ��
��![]() ������ֱ��
������ֱ��![]() ��ʱ�������
��ʱ�������![]() ���ܳ���
���ܳ���
��3����![]() ʱ��̽��
ʱ��̽��![]() ��
��![]() ��������ϵ��
��������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʫ�����ҹ��Ŵ��Ļ��еĹ屦��ij�н������ܲ���Ϊ�˽Ȿ�г�������ʫ�ʵ�ѧϰ������ٰ���һ�Ρ��л�ʫ�ʡ����д����������ȡ�˲���ͬѧ�ijɼ�(xΪ�������ܷ�100��)�������������в�������ͳ��ͼ����
��� | �ɼ�����(��λ����) | Ƶ�� |
A | 50��x��60 | 40 |
B | 60��x��70 | a |
C | 70��x��80 | 90 |
D | 80��x��90 | b |
E | 90��x��100 | 100 |
�ϼ� | c |
����������Ϣ����������⣺
(1)ͳ�Ʊ���a���� ����b���� ����c���� ����
(2)����ͳ��ͼ�У�m��ֵΪ�� ������E������Ӧ��Բ�ĽǵĶ������� �� (��)��
(3)���μӱ��δ�����ͬѧ����4000�ˣ�������Ƴɼ���80�ּ����ϵ�ѧ����Լ�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
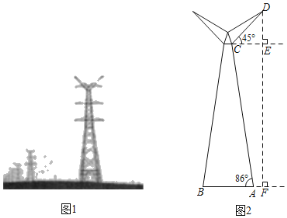
����Ŀ����ͼ��ʾ��ͼ1��ͼ2�ֱ���ij���ѹ������ʵ��ͼ��ʾ��ͼ�����ĵ���AB�����ƽ�룬DF��ʾ��������D������ľ��룬��֪AF�ij���2�ף�֧��AC�����нǡ�BAC��86�㣬����֧��DC��10�ף�DC��ˮƽ��CE֮��нǡ�DCE��45�㣬������ĸ߶�DF����sin86�㣽0.998��cos86�㣽0.070��tan86�㣽14.300��![]() ��1.4���������������
��1.4���������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
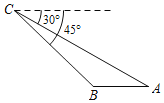
����Ŀ����ͼ����֪��C����һ���߿�̽�����ӵ�C�����ˮƽ������A��B����ĸ��Ƿֱ�Ϊ30����45������AB=2km����A��C����֮��ľ���Ϊ_____km��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳����������������֮����2400Ԫ����A��B�����˶�����22������֪����A���˶����빺��B���˶����ķ�����ͬ��A���˶����ĵ�����B���˶������۵�1.2����
��1����A��B�����˶����ĵ��۸��Ƕ���Ԫ��
��2�����ƻ��ò�����5600Ԫ���ʽ��ٴι���A��B�����˶�����50������֪A��B�����˶����Ľ��۲��䣮��A���˶�������ܹ������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
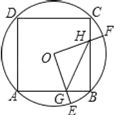
����Ŀ����ͼ���߳�Ϊ2��������ABCD�ڽ�����O����E��![]() ��һ�㣨����A��B�غϣ�����F��
��һ�㣨����A��B�غϣ�����F��![]() ��һ�㣬����OE��OF���ֱ���AB��BC���ڵ�G��B���ҡ�EOF��90�㣮�����н��ۣ���
��һ�㣬����OE��OF���ֱ���AB��BC���ڵ�G��B���ҡ�EOF��90�㣮�����н��ۣ���![]() ��
��![]() �����ı���OGBH��������ŵ�Eλ�õı仯���仯������GBH�ܳ�����СֵΪ2+
�����ı���OGBH��������ŵ�Eλ�õı仯���仯������GBH�ܳ�����СֵΪ2+![]() ������BG��1��
������BG��1��![]() ����BG��GE��
����BG��GE��![]() Χ�ɵ������
Χ�ɵ������![]() ��������ȷ����_____������������ȷ���۵���Ŷ����ϣ�
��������ȷ����_____������������ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
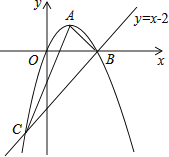
����Ŀ����ͼ����֪�����߾���ԭ��O������ΪA��1��1��������ֱ��y��x��2����B��C���㣮
��1���������ߵĽ���ʽ����B��C�����ꣻ
��2�����ABC������Բ�뾶��
��3������NΪx���ϵ�һ�����㣬����N��MN��x���������߽��ڵ�M�����Ƿ������O��M��NΪ��������������ABC���ƣ������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
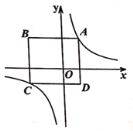
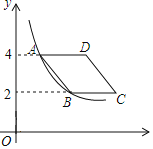
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�ڵ�һ�����ڣ���BC��x��ƽ�У�A��B�����������ֱ�Ϊ4��2������������y![]() ��x��0����ͼ��A��B���㣬������ABCD�����Ϊ2
��x��0����ͼ��A��B���㣬������ABCD�����Ϊ2![]() ����k��ֵΪ��������
����k��ֵΪ��������
A. 2B. 3C. 4D. 6
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com