
【题目】如图,二次函数![]() 的图象与y轴交于C点,交x轴于点A(-2,0),B(6,0),P是该函数在第一象限内图象上的动点,过点P作PQ⊥BC于点Q,连接PC,AC.
的图象与y轴交于C点,交x轴于点A(-2,0),B(6,0),P是该函数在第一象限内图象上的动点,过点P作PQ⊥BC于点Q,连接PC,AC.
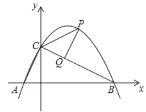
(1)求该二次函数的表达式;
(2)求线段PQ的最大值;
(3)是否存在点P,使得以点P,C,Q为顶点的三角形与△ACO相似?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)PQ的最大值为
;(2)PQ的最大值为![]() ;(3)
;(3)![]() 或
或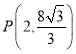
【解析】
(1)利用待定系数法,列出二元一次方程组求解即可得出结论;
(2)先确定出直线BC解析式,进而得出PM,再判断出△OAC∽△OCB,求出AC,进而得出∠MPQ的余弦值,即可得出结论;
(3)分两种情况,Ⅰ、当△QPC∽△OAC时,利用抛物线的对称性即可得出结论,Ⅱ、先确定出直线CD的解析式,联立抛物线解析式即可得出结论.
解:(1)将点A、B坐标代入抛物线解析式中得,
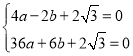 ,
,
∴解: ,
,
∴抛物线解析式为![]() ;
;
(2)设 ,
,![]()
令x=0,则![]() ,
,
∴![]() ,
,
∵B(6,0),
∴直线BC的解析式为![]() ,
,
如图1,过点P作PN⊥x轴于N,交BC于M,
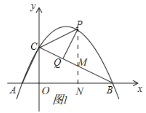
∴点 ,
,
∴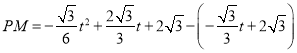
![]() ,
,
∵∠AOC=∠COB=∠CQP=∠POM=∠MDB=90°,
∵![]() ,
,
∴△OAC∽△OCB,
∴∠ACO=∠CBO=∠MPQ,
∴△OAC∽△OCB∽△NMB∽△QMP,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴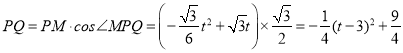
∴t=3时,PQ的最大值为![]() ;
;
(3)、①当△QPC∽△OAC时,
∴∠ACO=∠CBA=∠PCQ,
∴PC∥x轴,
由抛物线的对称性知,点C与点P关于P关于抛物线的对称轴对称,
∴![]() ;
;
②、当△QCP∽△OAC时,
∴∠CAO=∠PCQ,
∴tan∠CAO=tan∠PCQ,
如图2,过点B作BD⊥BC交CP的延长线于D,过点D作DE⊥x轴于E,
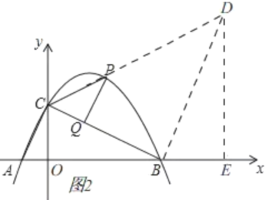
∴△OBC∽△EDB,
∴![]() ,
,
∴![]() ,
,
∴OE=OB+BE=12,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴直线CD的解析式为![]() ①
①
∵![]() ②,
②,
联立①②解得,
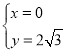 (舍)或
(舍)或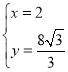 ,
,
∴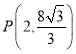 .
.


科目:初中数学 来源: 题型:
【题目】一套数学题集共有100道题,甲、乙和丙三人分别作答,每道题至少有一人解对,且每人都解对了其中的60道.如果将其中只有1人解对的题称作难题,2人解对的题称作中档题,3人都解对的题称作容易题,那么下列判断一定正确的是( )
A.容易题和中档题共60道B.难题比容易题多20道
C.难题比中档题多10道D.中档题比容易题多15道
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区统计了有扶贫任务的人员一个月下乡扶贫的天数(为整数),并制成了如下尚不完整的表格与条形统计图(如图).
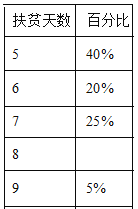
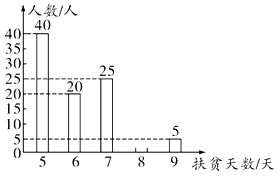
(1)有扶贫任务的人员的总人数是__________,并补全条形统计图;
(2)上级部门随机抽查1名扶贫人员,检查其工作情况,求抽查到的扶贫人员的扶贫天数大于7天的概率;
(3)若统计时漏掉1名扶贫人员,现将他的下乡天数和原统计的下乡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名扶贫人员下乡的天数最少是多少天.
查看答案和解析>>
科目:初中数学 来源: 题型:
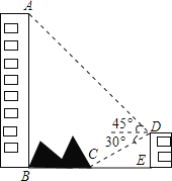
【题目】 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天能售出20件,每件盈利40元。经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件.设每件衬衫降价x元.
(1)降价后,每件衬衫的利润为_____元,销量为_____件;(用含x的式子表示)
(2)为了扩大销售,尽快减少库存,商场决定釆取降价措施。但需要平均每天盈利1200元,求每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
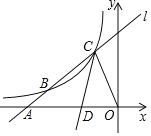
【题目】如图,直线l与反比例函数y=![]() (k≠0)的图象在第二象限交于B、C两点,与x轴交于点A,连接OC,∠ACO的角平分线交x轴于点D.若AB:BC:CO=1:2:2,△COD的面积为6,则k的值为______.
(k≠0)的图象在第二象限交于B、C两点,与x轴交于点A,连接OC,∠ACO的角平分线交x轴于点D.若AB:BC:CO=1:2:2,△COD的面积为6,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线l:y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,a).
(x>0)的图象交于点A(2,a).
(1)求a,k的值;
(2)横,纵坐标都是整数的点叫做整点.点P(m,n)为射线OA上一点,过点P作x轴,y轴的垂线,分别交函数y=![]() (x>0)的图象于点B,C.由线段PB,PC和函数y=
(x>0)的图象于点B,C.由线段PB,PC和函数y=![]() (x>0)的图象在点B,C之间的部分所围成的区域(不含边界)记为W.
(x>0)的图象在点B,C之间的部分所围成的区域(不含边界)记为W.
①若PA=OA,求区域W内的整点个数;
②若区域W内恰有5个整点,结合函数图象,直接写出m的取值范围.
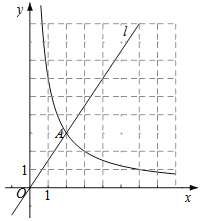
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张完全相同的卡片的正面分别画有等边三角形、平行四边形、矩形、菱形、正方形,将其背面朝上放在桌面上,从中随机抽取一张,所抽取的卡片上的图形既是轴对称图形,又是中心对称图形的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com