
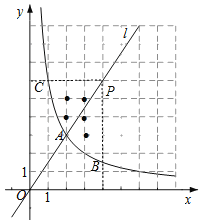
【题目】如图,在平面直角坐标系xOy中,直线l:y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,a).
(x>0)的图象交于点A(2,a).
(1)求a,k的值;
(2)横,纵坐标都是整数的点叫做整点.点P(m,n)为射线OA上一点,过点P作x轴,y轴的垂线,分别交函数y=![]() (x>0)的图象于点B,C.由线段PB,PC和函数y=
(x>0)的图象于点B,C.由线段PB,PC和函数y=![]() (x>0)的图象在点B,C之间的部分所围成的区域(不含边界)记为W.
(x>0)的图象在点B,C之间的部分所围成的区域(不含边界)记为W.
①若PA=OA,求区域W内的整点个数;
②若区域W内恰有5个整点,结合函数图象,直接写出m的取值范围.
【答案】(1)3,6;(2)①5个;②![]() 或
或![]() .
.
【解析】
(1)先根据直线的解析式可求a的值,从而可得点A的坐标,再将将点A坐标代入反比例函数的解析式可得k的值;
(2)①先求出点P坐标,再根据反比例函数的解析式求出点B、C坐标,然后结合函数图象、整点的定义即可得;
②分点P在点A下方和点P在点A上方两种情况讨论,结合函数图象列出不等式组求解即可.
(1)∵直线![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]()
∴![]()
∴![]()
将![]() 代入反比例函数
代入反比例函数![]() 得
得![]()
解得![]() ;
;
(2)①∵点P为射线OA上一点,且![]()
∴A为OP中点
∵![]()
![]() ,解得
,解得![]()
∴点P的坐标为![]()
将![]() 代入
代入![]() 得
得![]()
将![]() 代入
代入![]() 得
得![]() ,解得
,解得![]()
∵如图,PB,PC分别垂直于x轴和y轴
∴![]()
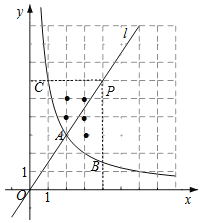
结合函数图象可知,区域W内有5个整点;
②![]() 在射线OA上
在射线OA上
![]()
由题意,分以下两种情况:
如图,当点P在点A下方时
结合函数图象得:![]() ,即
,即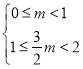
解得![]()
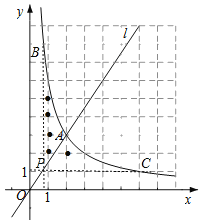
如图,当点P在点A上方时
结合函数图象得:![]() ,即
,即
解得![]()
综上,当![]() 或
或![]() 时,区域W内恰有5个整点.
时,区域W内恰有5个整点.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() ,
,![]() ,直线
,直线![]() .
.
(1)若该抛物线与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]() ,求该抛物线的顶点坐标;
,求该抛物线的顶点坐标;
(2)证明:该抛物线与直线![]() 必有两个交点;
必有两个交点;
(3)若该抛物线经过点![]() ,且对任意实数
,且对任意实数![]() ,不等式
,不等式![]() 都成立;当
都成立;当![]() 时,该二次函数的最小值为
时,该二次函数的最小值为![]() .求直线
.求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与y轴交于C点,交x轴于点A(-2,0),B(6,0),P是该函数在第一象限内图象上的动点,过点P作PQ⊥BC于点Q,连接PC,AC.
的图象与y轴交于C点,交x轴于点A(-2,0),B(6,0),P是该函数在第一象限内图象上的动点,过点P作PQ⊥BC于点Q,连接PC,AC.
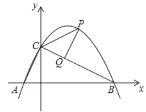
(1)求该二次函数的表达式;
(2)求线段PQ的最大值;
(3)是否存在点P,使得以点P,C,Q为顶点的三角形与△ACO相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春节联欢晚会传承创新亮点多,收视率较往年大幅增长.成都高新区某学校对部分学生就2020年春晚的关注程度,采用随机抽样调査的方式,并根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图(其中A表示“非常关注”;B表示“关注”;C表示“关注很少”;D表示“不关注”).
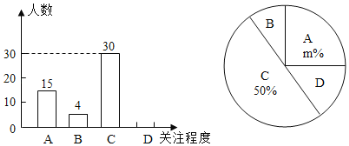
请你根据统计图中所提供的信息解答下列问题:
(1)直接写出m=______;估计该校1800名学生中“不关注”的人数是______人;
(2)在一次交流活动中,老师决定从本次调查回答“关注”的同学中随机选取2名同学来谈谈他们的想法,而本次调查回答“关注”的这些同学中只有一名男同学,请用画树状图或列表的方法求选取到两名同学中刚好有这位男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
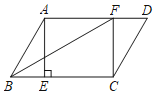
【题目】如图,ABCD中,点E,F分别在边BC,AD上,BE=DF,∠AEC=90°.
(1)求证:四边形AECF是矩形;
(2)连接BF,若AB=4,∠ABC=60°,BF平分∠ABC,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论:①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0;⑤(a+c)2<b2.其中,正确结论的个数是( )
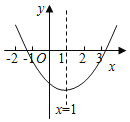
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江苏省常州市)为了解某校学生的课余兴趣爱好情况,某调查小组设计了“阅读”、“打球”、“书法”和“其他”四个选项,用随机抽样的方法调查了该校部分学生的课余兴趣爱好情况(每个学生必须选一项且只能选一项),并根据调查结果绘制了如下统计图:

根据统计图所提供的信息,解答下列问题:
(1)本次抽样调查中的样本容量是 ;
(2)补全条形统计图;
(3)该校共有2000名学生,请根据统计结果估计该校课余兴趣爱好为“打球”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com