练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

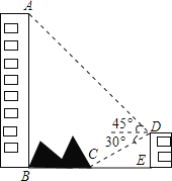
    【题目】 如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=80m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据：≈1.414，≈1.732）

    【答案】52.7m

    【解析】

    如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．通过解直角△AFD得到DF的长度；通过解直角△DCE得到CE的长度，则BC=BE-CE．

    解：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．

    则DE=BF=CH=10m，

    在直角△ADF中，∵AF=80m-10m=70m，∠ADF=45°，

    ∴DF=AF=70m．

    在直角△CDE中，∵DE=10m，∠DCE=30°，

    ∴CE===10（m），

    ∴BC=BE-CE=70-10≈70-17.32≈52.7（m）．

    答：障碍物B，C两点间的距离约为52.7m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

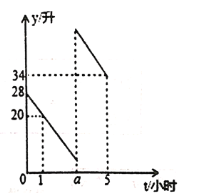
    【题目】李师傅驾车从甲地到乙地，途中在加油站加了一次油，加油时，车载电脑显示油箱中剩余油量4升，已知汽车行驶时，每小时耗油量一定，设油箱中剩余油量为（升），汽车行驶时间为（时）,与之间的函数图像如图所示．

    （1）求李师傅加油前与之间的函数关系式；

    （2）求的值；

    （3）李师傅在加油站的加油量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的直径AB＝26，P是AB上(不与点A、B重合)的任一点，点C、D为⊙O上的两点，若∠APD＝∠BPC，则称∠CPD为直径AB的“回旋角”．

    (1)若∠BPC＝∠DPC＝60°，则∠CPD是直径AB的“回旋角”吗？并说明理由；

    (2)若的长为π，求“回旋角”∠CPD的度数；

    (3)若直径AB的“回旋角”为120°，且△PCD的周长为24+13，直接写出AP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】社区利用一块矩形空地建了一个小型的惠民停车场，其布局如图所示.已知停车场的长为52米，宽为28米，阴影部分设计为停车位，要铺花砖，其余部分是等宽的通道.已知铺花砖的面积为640平方米.

    （1）求通道的宽是多少米？

    （2）该停车场共有车位64个，据调查分析，当每个车位的月租金为200元时，可全部租出；当每个车位的月租金每上涨10元，就会少租出1个车位.当每个车位的月租金上涨多少元时，停车场的月租金收入为14400元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

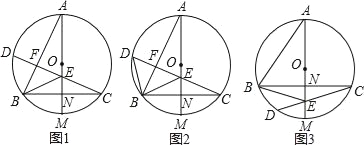
    【题目】已知AM是⊙O直径，弦BC⊥AM，垂足为点N，弦CD交AM于点E，连按AB和BE．

    （1）如图1，若CD⊥AB，垂足为点F，求证：∠BED＝2∠BAM；

    （2）如图2，在（1）的条件下，连接BD，若∠ABE＝∠BDC，求证：AE＝2CN；

    （3）如图3，AB＝CD，BE：CD＝4：7，AE＝11，求EM的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

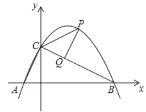
    【题目】如图，二次函数的图象与y轴交于C点，交x轴于点A（-2，0），B（6，0），P是该函数在第一象限内图象上的动点，过点P作PQ⊥BC于点Q，连接PC，AC．

    （1）求该二次函数的表达式；

    （2）求线段PQ的最大值；

    （3）是否存在点P，使得以点P，C，Q为顶点的三角形与△ACO相似？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点到直线的距离即为点到直线的垂线段的长．

    （1）如图1，取点M（1，0），则点M到直线l：y＝x﹣1的距离为多少？

    （2）如图2，点P是反比例函数y＝在第一象限上的一个点，过点P分别作PM⊥x轴，作PN⊥y轴，记P到直线MN的距离为d0，问是否存在点P，使d0＝？若存在，求出点P的坐标，若不存在，请说明理由．

    （3）如图3，若直线y＝kx+m与抛物线y＝x2﹣4x相交于x轴上方两点A、B（A在B的左边）．且∠AOB＝90°，求点P（2，0）到直线y＝kx+m的距离最大时，直线y＝kx+m的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

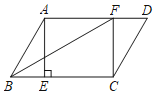
    【题目】如图，ABCD中，点E，F分别在边BC，AD上，BE＝DF，∠AEC＝90°．

    （1）求证：四边形AECF是矩形；

    （2）连接BF，若AB＝4，∠ABC＝60°，BF平分∠ABC，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了解八年级学生参加社会实践活动情况，随机调查了本校部分八年级学生在第一学期参加社会实践活动的天数，并用得到的数据绘制了统计图①和图②，请根据图中提供的信息，回答下列问题：

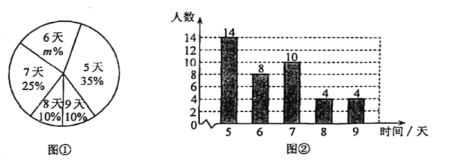
    （1）本次接受随机抽样调查的学生人数为 ，图①中的的值为 ；

    （2）求本次抽样调查获取的样本数据的众数、中位数和平均数；

    （3）若该校八年级学生有人，估计参加社会实践活动时间大于天的学生人数．

    查看答案和解析>>

    同步练习册答案