
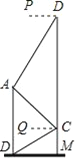
【题目】如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据: ![]() ≈1.73).
≈1.73).
【答案】雕塑AB的高约是6.3m.
【解析】试题分析:过A作AR⊥DM,垂足是R,在Rt△ARD中利用三角函数求得AR的长,延长CQ交AB于点N,在Rt△ANC中利用三角函数求得AN的长,在Rt△CNB中求得NB的长,根据AB=BN+AN求解.
试题解析:过A作AR⊥DM,垂足是R.
∵∠PDA=60°,∴∠ADR=30°,
在Rt△ARD中,AR=ADsin30°=8×![]() =4(m),
=4(m),
延长CQ交AB于点N.
在Rt△ANC中,∠ANC=90°,∠ACN=45°,∴AN=NC=AR=4(m),
在Rt△CNB中,∠CNB=90°,∠NCB=30°,∴NB=CNtan30°=4×![]() =
=![]() (m).
(m).
∴AB=BN+AN=![]() +4≈6.3(m).
+4≈6.3(m).
答:雕塑AB的高约是6.3m.



 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】小明总结了以下结论:①a(b+c)=ab+ac;②a(b﹣c)=ab﹣ac;③(b﹣c)÷a=b÷a﹣c÷a(a≠0);④a÷(b+c)=a÷b+a÷c(a≠0);其中一定成立的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知线段MN的两个端点的坐标分别是M(-4,-1)、N(0,1),将线段MN平移后得到线段M ′N ′(点M、N分别平移到点M ′、N ′的位置),若点M ′的坐标为(-2,2),则点N ′的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. 2m(m-1)=2m2-1 B. (m+1)2=m2+1 C. (m-2)(m+2)=m2-4 D. 6m6÷3m2=2m3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( ) 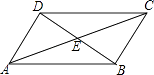
A.6
B.12
C.20
D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.—2是4的一个平方根B.立方根等于它本身的数只有1和0
C.平方根等于它本身的数只有0D.平方等于它本身的数只有0和1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com