
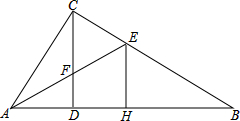
 如图,△ABC中,∠ACB=90°,CD⊥AB于点D,E为BC上一点,AE交CD于点F,EH⊥AB于点H,若CF=2FD,EH=$\sqrt{2}$,求CE•BE的值.
如图,△ABC中,∠ACB=90°,CD⊥AB于点D,E为BC上一点,AE交CD于点F,EH⊥AB于点H,若CF=2FD,EH=$\sqrt{2}$,求CE•BE的值. 分析 要求两条线段的乘积,而题目当中只告诉了线段EH的长度,因此只需将两条线段分别用其它线段的式子表示出来,再代入相乘,化简转化为关于EH的式子.而进行线段关系的转化,必然需要几何等式,结合题设条件,本题可以列出的等式有相似三角形的线段比例等式(△ADC∽△EHB)、射影定理(实质上也是相似)、梅涅劳斯定理(直线AFE截△BDC),将相应的与CE、BE相关的等式列出进综合运算化简即可得解.
解答 解:对于△CBD和截线AFE,由梅涅劳斯定理可知:$\frac{CE}{EB}•\frac{BA}{AD}•\frac{DF}{FC}=1$,
∵CF=2FD,
∴$\frac{FD}{CF}=\frac{1}{2}$,
∴$CE=2•\frac{AD}{AB}•BE$,
易知△ADC∽△EHB,
∴$\frac{BE}{AC}=\frac{EH}{AD}$,
∴$BE=\frac{EH}{AD}•AC$,
由射影定理可知AC2=AD•AB,
∴BE•CE=$(2•\frac{AD}{AB}•BE)•BE=2•\frac{AD}{AB}•B{E}^{2}$=$2•\frac{AD}{AB}•(\frac{EH}{AD}•AC)^{2}=2•\frac{AD}{AB}•\frac{E{H}^{2}}{A{D}^{2}}•A{C}^{2}$=$2•\frac{AD}{AB}•\frac{E{H}^{2}}{A{D}^{2}}•AD•AB=2E{H}^{2}$,
∵EH=$\sqrt{2}$,
∴BE•CE=4.
点评 本题主要考查相似三角形的判定与性质、射影定理、梅涅劳斯定理的应用.难度并不大,并不需要辅助线,只不过需要进行稍微复杂的线段运算化简.题目设计巧妙,是一道好题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
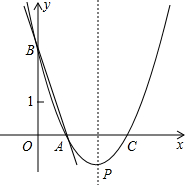 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B.求:
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
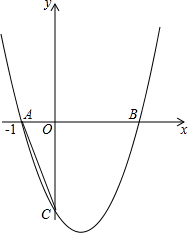 已知,如图,抛物线y=x2+bx+c的图象经过点A(-1,0),该抛物线与x轴的另一交点为B,与y轴的交点为C,tan∠CAO=3.
已知,如图,抛物线y=x2+bx+c的图象经过点A(-1,0),该抛物线与x轴的另一交点为B,与y轴的交点为C,tan∠CAO=3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-1 | B. | x+1 | C. | $\frac{{x}^{2}+1}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com