
 如图,正方形ABCD中内接正三角形AEF.求证:S△EFC=S△ABE+S△ADF.
如图,正方形ABCD中内接正三角形AEF.求证:S△EFC=S△ABE+S△ADF. 分析 首先连接AC,交EF于点G,易证得Rt△ABE≌Rt△ADF(HL);继而证得AC垂直平分EF,然后设EC=x,再表示出各三角形的面积,即可证得结论.
解答 证明:∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
∵△AEF是等边三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$,
∴Rt△ABE≌Rt△ADF(HL);
∴BE=DF,
连接AC,交EF于点G,
∵BC=CD,BE=DF
∴BC-BE=CD-DF,即CE=CF,
又∵AE=AF,
∴AC垂直平分EF.
设EC=x,由勾股定理,得EF=$\sqrt{E{C}^{2}+F{C}^{2}}$=$\sqrt{2}$x,
由直角三角形斜边上中线的性质可知:CG=$\frac{1}{2}$EF=$\frac{\sqrt{2}}{2}$x,
在Rt△AEG中,AG=AEsin60°=EFsin60°=2×CGsin60°=$\frac{\sqrt{6}}{2}$x,
∴AC=AG+CG=$\frac{\sqrt{2}+\sqrt{6}}{2}$x,
∴AB=$\frac{\sqrt{2}}{2}$AC=$\frac{1+\sqrt{3}}{2}$x,
∴BE=BC-CE=$\frac{1+\sqrt{3}}{2}$x-x=$\frac{\sqrt{3}-1}{2}$x,
∴S△CEF=$\frac{1}{2}$EC•CF=$\frac{1}{2}$x2,S△ABE=$\frac{1}{2}$×$\frac{1+\sqrt{3}}{2}$x×$\frac{\sqrt{3}-1}{2}$x=$\frac{1}{4}$x2,
∴S△ADF=S△ABE=$\frac{1}{4}$x2,
∴S△ABE+S△ADF=S△CEF.
点评 此题考查了正方形的性质、全等三角形的判定与性质、线段垂直平分线的性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
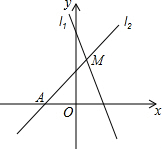 如图,已知直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )
如图,已知直线l1:y=-2x+4与直线l2:y=kx+b(k≠0)在第一象限交于点M.若直线l2与x轴的交点为A(-2,0),则k的取值范围是( )| A. | -2<k<2 | B. | -2<k<0 | C. | 0<k<4 | D. | 0<k<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
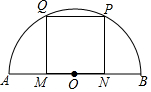 如图,点M,N在半圆的直径AB上,点P,Q在$\widehat{AB}$上,四边形MNPQ为正方形.若半圆的半径为$\sqrt{5}$,则正方形的边长为2.
如图,点M,N在半圆的直径AB上,点P,Q在$\widehat{AB}$上,四边形MNPQ为正方形.若半圆的半径为$\sqrt{5}$,则正方形的边长为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
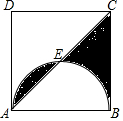 小明向如图所示的正方形ABCD区域内投掷飞镖,点E是以AB为直径的半圆与对角线AC的交点.如果小明投掷飞镖一次,则飞镖落在阴影部分的概率为( )
小明向如图所示的正方形ABCD区域内投掷飞镖,点E是以AB为直径的半圆与对角线AC的交点.如果小明投掷飞镖一次,则飞镖落在阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
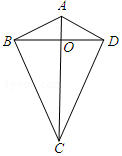 两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有( )
两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有( )| A. | ①③⑤ | B. | ①③④ | C. | ③④⑤ | D. | ①④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
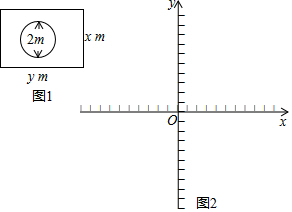 2016年11月28日,神州十一号返回舱成功着陆.假如返回舱着陆后A地为一个直径为2m的圆形,工作人员用警戒带在其外围至少1米外圈成一个面积为80m2的长方形,其俯视如图1所示.设长方形的长为ym,宽为xm.
2016年11月28日,神州十一号返回舱成功着陆.假如返回舱着陆后A地为一个直径为2m的圆形,工作人员用警戒带在其外围至少1米外圈成一个面积为80m2的长方形,其俯视如图1所示.设长方形的长为ym,宽为xm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com