
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+2ЃЈaЁй0ЃЉгыxжсНЛгкAЃЈ4ЃЌ0ЃЉЁЂBЃЈЉ1ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЌВЂаДГіЦфЖдГЦжсЃЛ
ЃЈ2ЃЉАбЃЈ1ЃЉжаЫљЧѓГіЕФХзЮяЯпМЧЮЊC1ЃЌНЋC1ЯђгвЦНвЦmИіЕЅЮЛЕУЕНХзЮяЯпC2ЃЌC1гыC2ЕФдкЕквЛЯѓЯоНЛЕуЮЊMЃЌЙ§ЕуMзїMGЁЭxжсгкЕуGЃЌНЛЯпЖЮACгкЕуHЃЌСЌНгCMЃЌЕБЁїCMHЮЊЕШбќШ§НЧаЮЪБЃЌЧѓХзЮяЯпЯђгвЦНвЦЕФОрРыmКЭДЫЪБЕуMЕФзјБъЃЎ

ЁОД№АИЁП(1)ЁЂy=Љ![]() x2+
x2+![]() x+2ЃЌЖдГЦжсЪЧЃКжБЯпx=
x+2ЃЌЖдГЦжсЪЧЃКжБЯпx=![]() ЃЛ(2)ЁЂm=1ЃЌMЃЈ2ЃЌ3ЃЉ.
ЃЛ(2)ЁЂm=1ЃЌMЃЈ2ЃЌ3ЃЉ.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃК(1)ЁЂРћгУНЛЕуЪНЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЌВЂХфЗНЧѓЖдГЦжсЃЛ(2)ЁЂЯШЧѓжБЯпACЕФНтЮіЪНЃЌИљОнИїздЕФНтЮіЪНЩшГіMЃЈxЃЌЉ![]() x2+
x2+![]() +2ЃЉЃЌHЃЈxЃЌЉ
+2ЃЉЃЌHЃЈxЃЌЉ![]() x+2ЃЉЃЌгЩЭМЕУЁїCMHЮЊЕШбќШ§НЧаЮЪБЃЌCM=CHЃЌдђгаGH+GM=4ЃЌСаЪНМЦЫуЧѓГіMЕФзјБъЃЌАбMЕФзјБъДњШыЦНвЦКѓЕФНтЮіЪНПЩВЂЕУГіmЕФжЕЃЎ
x+2ЃЉЃЌгЩЭМЕУЁїCMHЮЊЕШбќШ§НЧаЮЪБЃЌCM=CHЃЌдђгаGH+GM=4ЃЌСаЪНМЦЫуЧѓГіMЕФзјБъЃЌАбMЕФзјБъДњШыЦНвЦКѓЕФНтЮіЪНПЩВЂЕУГіmЕФжЕЃЎ
ЪдЬтНтЮіЃК(1)ЁЂЕБx=0ЪБЃЌy=ax2+bx+2=2ЃЌ ЁрХзЮяЯпОЙ§ЃЈ0ЃЌ2ЃЉЃЌ
ЁпХзЮяЯпy=ax2+bx+2ЃЈaЁй0ЃЉгыxжсНЛгкAЃЈ4ЃЌ0ЃЉЁЂBЃЈЉ1ЃЌ0ЃЉСНЕуЃЌ
ЩшХзЮяЯпЕФНтЮіЪНЮЊЃКy=aЃЈxЉ4ЃЉЃЈx+1ЃЉЃЌ АбЃЈ0ЃЌ2ЃЉДњШыЕУЃК2=aЃЈ0Љ4ЃЉЃЈ0+1ЃЉЃЌ a=Љ![]() ЃЌ
ЃЌ
Ёрy=Љ![]() ЃЈxЉ4ЃЉЃЈx+1ЃЉ=Љ
ЃЈxЉ4ЃЉЃЈx+1ЃЉ=Љ![]() x2+
x2+![]() +2=Љ
+2=Љ![]() ЃЈxЉ
ЃЈxЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКy=Љ![]() x2+
x2+![]() +2ЃЌЖдГЦжсЪЧЃКжБЯпx=
+2ЃЌЖдГЦжсЪЧЃКжБЯпx=![]() ЃЛ
ЃЛ
(2)ЁЂЩшжБЯпACЕФНтЮіЪНЮЊЃКy=kx+bЃЌ АбAЃЈ4ЃЌ0ЃЉЁЂCЃЈ0ЃЌ2ЃЉДњШыЕУЃК![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК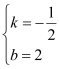 ЃЌ
ЃЌ
ЁржБЯпACЕФНтЮіЪНЮЊЃКy=Љ![]() x+2ЃЌ ЩшMЃЈxЃЌЉ
x+2ЃЌ ЩшMЃЈxЃЌЉ![]() x2+
x2+![]() +2ЃЉЃЌHЃЈxЃЌЉ
+2ЃЉЃЌHЃЈxЃЌЉ![]() x+2ЃЉЃЌ
x+2ЃЉЃЌ
ЁпЁїCMHЮЊЕШбќШ§НЧаЮЃЌ ЁрCM=CHЃЌ ЁрCЪЧMHДЙжБЦНЗжЯпЩЯЕФЕуЃЌ ЁрGH+GM=4ЃЌ
дђЉ![]() x2+
x2+![]() +2+ЃЈЉ
+2+ЃЈЉ![]() x+2ЃЉ=4ЃЌ НтЕУЃКx1=0ЃЈЩсЃЉЃЌx2=2ЃЌ ЁрMЃЈ2ЃЌ3ЃЉЃЌ
x+2ЃЉ=4ЃЌ НтЕУЃКx1=0ЃЈЩсЃЉЃЌx2=2ЃЌ ЁрMЃЈ2ЃЌ3ЃЉЃЌ
ЩшЦНвЦКѓЕФХзЮяЯпЕФНтЮіЪНЮЊЃКy=Љ![]() ЃЈxЉ
ЃЈxЉ![]() ЉmЃЉ2+
ЉmЃЉ2+![]() ЃЌ АбMЃЈ2ЃЌ3ЃЉДњШыЕУЃКm=1ЃЎ
ЃЌ АбMЃЈ2ЃЌ3ЃЉДњШыЕУЃКm=1ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=CBЃЌЁЯABC=90ЁуЃЌFЮЊABбгГЄЯпЩЯвЛЕуЃЌЕуEдкBCЩЯЃЌЧвAE=CFЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїABEЁеЁїCBFЃЛ
ЃЈ2ЃЉШєЁЯCAE=30ЁуЃЌЧѓЁЯACFЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=ax2+bx+cЃЈaЁй0ЃЉЕФЭМЯѓгыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌЧвOA=OCЃЌдђЯТСаНсТлЂйabcЃМ0ЃЛЂкb2Љ4acЃО0ЃЛЂлacЉb+1=0ЃЛЂмOAOB=![]() ЃЎЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
ЃЎЦфжае§ШЗНсТлЕФИіЪ§ЪЧЃЈ ЃЉ
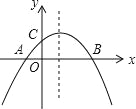
AЃЎ1 BЃЎ2 CЃЎ3 DЃЎ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈx+yЃЉЃЈx+y+2ЃЉ-8=0ЃЌдђx+yЕФжЕЪЧЃЈЁЁЁЁЃЉ
A.-4Лђ2
B.-2Лђ4
C.2Лђ-3
D.3Лђ-2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛЫвДЌДгМзТыЭЗЕНввТыЭЗЫГСїЖјааЃЌгУСЫ3аЁЪБЃЌДгввТыЭЗЗЕЛиМзТыЭЗФцСїЖјЩЯЃЌЖргУСЫ1.5аЁЪБЃЎвбжЊЫЎСїЕФЫйЖШЪЧ4km/hЃЌЩшДЌдкОВЫЎжаЕФЦНОљЫйЖШЮЊx km/hЃЌПЩСаЗНГЬЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃМЦЛЎгУ104 000дЊЙКжУвЛХњЕчФдЃЈетХњПюЯюаыЧЁКУгУЭъЃЌВЛЕУЪЃгрЛђзЗМгЃЉЃЎОЙ§еаБъЃЌЦфжаЦНАхЕчФдУПЬЈ1600дЊЃЌЬЈЪНЕчФдУПЬЈ4000дЊЃЌБЪМЧБОЕчФдУПЬЈ4600дЊЃЎ
ЃЈ1ЃЉШєбЇаЃЭЌЪБЙКНјЦфжаСНжжВЛЭЌРраЭЕФЕчФдЙВ50ЬЈЃЌЧыФуАябЇаЃЩшМЦИУШчКЮЙКТђЃЛ
ЃЈ2ЃЉШєбЇаЃЭЌЪБЙКНјШ§жжВЛЭЌРраЭЕФЕчФдЙВ26ЬЈЃЈШ§жжРраЭЕФЕчФдЖМгаЃЉЃЌВЂЧввЊЧѓБЪМЧБОЕчФдЕФЙКТђСПВЛЩйгк15ЬЈЃЌЧыФуАябЇаЃЩшМЦЙКТђЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЧЦкЬьаЁРюВНааШЁЭМЪщЙнПДЪщЃЌЭОжагіЕНвЛИіКьЕЦЃЌЭЃЯТРДЕЂЮѓСЫМИЗжжгЃЌЮЊСЫИЯЪБМфЃЌЫћвдИќПьЫйЖШВНааЕНЭМЪщЙнЃЌЯТУцМИЗљЭМЪЧВНааТЗГЬsЃЈУзЃЉгыааНјЪБМфtЃЈЗжЃЉЕФЙиЯЕЕФЪОвтЭМЃЌФуШЯЮЊе§ШЗЕФЪЧЃЈ ЃЉ
A.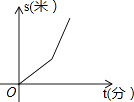
B.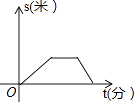
C.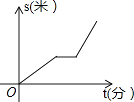
D.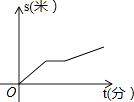
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖЏЕуPвд2cm/sЕФЫйЖШбиЭМ1ЫљЪОЕФБпПђДгBЁњCЁњDЁњEЁњFЁњAЕФТЗОЖдЫЖЏЃЌМЧЁїABPЕФУцЛ§ЮЊtЃЈcm2ЃЉЃЌyгыдЫЖЏЪБМфtЃЈsЃЉЕФЙиЯЕШчЭМ2ЫљЪОЃЎ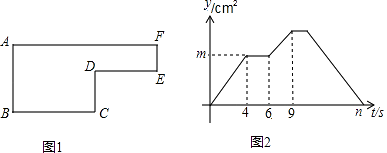
ШєAB=6cmЃЌЧыЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓЭМ1жаBCЁЂCDЕФГЄМАБпПђЫљЮЇГЩЭМаЮЕФУцЛ§ЃЛ
ЃЈ2ЃЉЧѓЭМ2жаmЁЂnЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com