
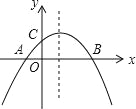
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论①abc<0;②b2﹣4ac>0;③ac﹣b+1=0;④OAOB=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
【答案】C
【解析】
试题分析:利用抛物线开口方向得到a<0,利用抛物线的对称轴位置得到b<0,利用抛物线与y轴的交点位置得到c<0,则可对①进行判断;利用抛物线与x轴有2个交点可对②进行判断;把A点坐标代入解析式可对③进行判断;设A、B两点的横坐标为x1、x2,则OA=﹣x1,OB=x2,利用根与系数的关系可对④进行判断. ∵抛物线开口向下, ∴a<0, ∵抛物线的对称轴在y轴的右侧, ∴b<0,
∵抛物线与y轴的交点在x轴下方, ∴c<0, ∴abc<0,所以①正确;∵抛物线与x轴有2个交点,
∴△=b2﹣4ac>0,所以②正确; ∵OA=OC,C(0,c), ∴A(﹣c,0), ∴ac2﹣bc+c=0,
∴ac﹣b+1=0,所以③正确; 设A、B两点的横坐标为x1、x2,则OA=﹣x1,OB=x2, ∵x1x2=![]() ,
,
∴OAOB=﹣![]() ,所以④错误.
,所以④错误.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如果∠1与∠2互为余角,∠1与∠3互为补角,那么下列结论: ①∠3﹣∠2=90° ②∠3+∠2=270°﹣2∠1 ③∠3﹣∠1=2∠2 ④∠3>∠1+∠2.
正确的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2是关于x的方程x2-2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为( )
A.10
B.14
C.10或14
D.8或10
查看答案和解析>>
科目:初中数学 来源: 题型:
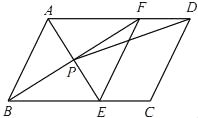
【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正常字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)扇形统计图中“C组”所对应的圆心角的度数是 ;
(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=120°,AD平分∠BAC,且AD=4,点P是射线AB上一动点,连接DP,△PAD的外接圆于AC交于点Q,则线段QP的最小值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若△ABC与△DEF全等,A和D,B和F分别是对应顶点,下列结论正确的是( )
A. AB=DE B. ∠A=∠D C. ∠B=∠E D. AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,与y轴交于点C.
(1)求抛物线的解析式,并写出其对称轴;
(2)把(1)中所求出的抛物线记为C1,将C1向右平移m个单位得到抛物线C2,C1与C2的在第一象限交点为M,过点M作MG⊥x轴于点G,交线段AC于点H,连接CM,当△CMH为等腰三角形时,求抛物线向右平移的距离m和此时点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com