练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

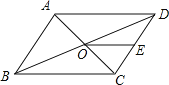
    【题目】如图，ABCD的周长为36，对角线AC，BD相交于点O．点E是CD的中点，BD=12，则△DOE的周长为 ______ ．

    【答案】15

    【解析】试题分析：根据平行四边形的对边相等和对角线互相平分可得，OB=OD，又因为E点是CD的中点，可得OE是△BCD的中位线，可得OE=BC，所以易求△DOE的周长．

    解：∵ABCD的周长为36，

    ∴2（BC+CD）=36，则BC+CD=18．

    ∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，BD=12，

    ∴OD=OB=BD=6．

    又∵点E是CD的中点，

    ∴OE是△BCD的中位线，DE=CD，

    ∴OE=BC，

    ∴△DOE的周长=OD+OE+DE=BD+（BC+CD）=6+9=15，

    即△DOE的周长为15．

    故答案为：15．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】用适当的方法解下列方程：

    （1）（2x+1）2=（x﹣1）2

    （2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（ ）

    A．m3+m3=m6 B．m3m2=m6 C．（m3）2=m5 D．m3÷m2=m

    查看答案和解析>>

    科目：初中数学 来源： 题型：

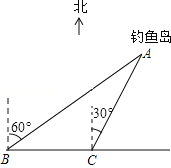
    【题目】如图，我国的一艘海监船在钓鱼岛A附近沿正东方向航行，船在B点时测得钓鱼岛A在船的北偏东60°方向，船以50海里/时的速度继续航行2小时后到达C点，此时钓鱼岛A在船的北偏东30°方向．请问船继续航行 海里与钓鱼岛A的距离最近？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】孙杨正在为备战第15届游泳世锦赛而刻苦训练．为判断他的成绩是否稳定，教练要对他10次训练的成绩进行统计分析，则教练需了解10次成绩的（ ）

    A．众数 B．方差 C．平均数 D．频数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校九年级两个班各为玉树地震灾区捐款1800元．已知2班比1班人均捐款多4元，2班的人数比1班的人数少10%．请你根据上述信息，就这两个班级的“人数”或“人均捐款”提出一个用分式方程解决的问题，并写出解题过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【观察发现】

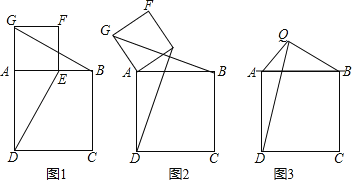
    如图1，四边形ABCD和四边形AEFG都是正方形，且点E在边AB上，连接DE和BG，猜想线段DE与BG的数量关系，以及直线DE与直线BG的位置关系．（只要求写出结论，不必说出理由）

    【深入探究】

    如图2，将图1中正方形AEFG绕点A逆时针旋转一定的角度，其他条件与观察发现中的条件相同，观察发现中的结论是否还成立？请根据图2加以说明．

    【拓展应用】

    如图3，直线l上有两个动点A、B，直线l外有一点O，连接OA，OB，OA，OB长分别为、4，以线段AB为边在l的另一侧作正方形ABCD，连接OD．随着动点A、B的移动，线段OD的长也会发生变化，在变化过程中，线段OD的长是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=3，AD=1，点P在线段AB上运动，设AP=x，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原．

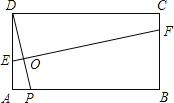
    （1）当点E与点A重合时，折痕EF的长为 ；

    （2）写出使四边形EPFD为菱形的x的取值范围，并求出当x=2时菱形的边长；

    （3）令EF2=y，当点E在AD、点F在BC上时，写出y与x的函数关系式（写出x的取值范围）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在以下现象中：①在笔直的公路上行驶的汽车；②用打气筒给自行车打气时，气筒里活塞的运动；③随风摆动的旗帜；④小河里流动的水流．属于平移的是( )

    ① 　B.①② C.①②③　 D.①②③④

    查看答案和解析>>

    同步练习册答案