Question

【题目】如图，在矩形ABCD中，AB=3，AD=1，点P在线段AB上运动，设AP=x，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原．

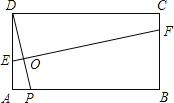
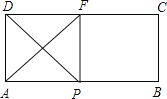
（1）当点E与点A重合时，折痕EF的长为 ；

（2）写出使四边形EPFD为菱形的x的取值范围，并求出当x=2时菱形的边长；

（3）令EF2=y，当点E在AD、点F在BC上时，写出y与x的函数关系式（写出x的取值范围）．

Answer 1

【答案】（1）；（2）m=1.25，此时菱形EPFD的边长为1.25；（3）0≤x≤3﹣2．

【解析】

试题分析：（1）当点E与点A重合时，得出∠DEF=∠FEP=45°，利用勾股定理得出答案即可；

（2）结合EF的长度得出x的取值范围，当x=2时，设PE=m，则AE=2﹣m，利用勾股定理得出答案；

（3）构造直角三角形，利用相似三角形的对应线段成比例确定y的值．

解：（1）∵纸片折叠，使点D与点P重合，得折痕EF，

当点E与点A重合时，

∵点D与点P重合是已知条件，

∴∠DEF=∠FEP=45°，

∴∠DFE=45°，即：ED=DF=1，

利用勾股定理得出EF=，

∴折痕EF的长为 ．

故答案为：；

（2）∵要使四边形EPFD为菱形，

∴DE=EP=FP=DF，

只有点E与点A重合时，EF最长为，此时x=1，

当EF最长时，点P与B重合，此时x=3，

∴探索出1≤x≤3

当x=2时，如图，连接DE、PF．

∵EF是折痕，

∴DE=PE，设PE=m，则AE=2﹣m

∵在△ADE中，∠DAP=90°，

∴AD2+AE2=DE2，即12+（2﹣m）2=m2，

解得 m=1.25，此时菱形EPFD的边长为1.25；

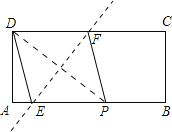
（3）过E作EH⊥BC；

∵∠EDO+∠DOE=90°，∠FEO+∠EOD=90°，

∴∠ODE=∠FEO，

∴△EFH∽△DPA，

∴，

∴FH=3x；

∴y=EF2=EH2+FH2=9+9x2；

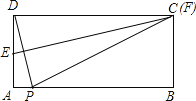
当F与点C重合时，如图，连接PF；

∵PF=DF=3，

∴PB=，

∴0≤x≤3﹣2．