
����Ŀ����֪����ͼA��B�ֱ�Ϊ�����ϵ����㣬A���Ӧ����Ϊ��10��B���Ӧ����Ϊ70 ![]()
��1����д��AB���е�M��Ӧ����
��2��������һֻ��������P��A���������3����λ/����ٶ������˶���ͬʱ��һֻ��������Qǡ�ô�B���������2����λ/����ٶ������˶�������ֻ���������������ϵ�C���������������C���Ӧ����
��3��������������P��A���������3����λ/����ٶ������˶���ͬʱ��һֻ��������Qǡ�ô�B���������2��λ/����ٶ������˶��������ʱ����ֻ�������������������35����λ���ȣ���д����ʱP���Ӧ������
���𰸡�
��1���⣺M���Ӧ�����ǣ���10+70����2=30
��2���⣺��A��B�ֱ�Ϊ�����ϵ����㣬A���Ӧ����Ϊ��10��B���Ӧ����Ϊ70��
��AB=70+10=80��
��t���P��Q������
��3t+2t=80�����t=16��
���ʱ��Q�߹���·��=3��16=48��
���ʱC���ʾ����Ϊ��10+48=38��
��C���Ӧ������38
��3���⣺����ǰ����80��35���£�2+3��=9���룩��
������35+80���£�2+3��=23���룩��
��9���23�룬2ֻ�������������������35����λ���ȣ�9���Ӧ����Ϊ17��23���Ӧ����Ϊ59
����������1����10��70�͵�һ�뼴��M��Ӧ��������2�������AB�ij�������t���P��Q�������ɵó�����t��һԪһ�η��̣����t��ֵ�������P��Q����ʱ��Q�ƶ��ľ��룬�����ɵó�C���Ӧ��������3����Ϊ2ֻ������������ǰ���35����λ���Ⱥ����������35����λ���ȣ�����ǰ����80��35���£�2+3��=9���룩��������35+80���£�2+3��=23���룩��
�����㾫����������Ĺؼ�����������������֪ʶ�����������ǹ涨��ԭ�㡢������λ���ȵ�һ��ֱ�ߣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.x+y��һ�ε���ʽ
B.����ʽ3��a3+4a2��8�Ĵ�����4
C.x��ϵ���ʹ�������1
D.����ʽ4��104x2��ϵ����4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������¼�������¼����ǣ� ��
A.�����������㻭һ��ֱ��B.���⻭һ������Σ�����Ǻ�Ϊ360��
C.��ƽ�������������㻭һ��ԲD.���⻭һ��ƽ���ı��Σ������ĶԳ�ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������˾�Ŀ�ݳ��ͻ���ͬʱ�Ӽس������Ը��Ե��ٶ��������ҵ���ʻ����ݳ������ҵغ�ж����Ʒ����װ������װж���ﹲ��45 min��������ԭ·����һ�ٶ����ٷ�����ֱ���������������֪�������ٶ�Ϊ60 km/h������֮��ľ���y(km)�������ʻʱ��x(h)֮��ĺ���ͼ����ͼ��ʾ�������н��ۣ�����ݳ��Ӽص��ҵص��ٶ�Ϊ100 km/h�����ס�������֮��ľ���Ϊ120 km����ͼ�е�B������Ϊ(3.75��75)������ݳ����ҵط���ʱ���ٶ�Ϊ90 km/h.������ȷ����( )
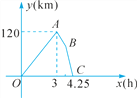
A. �٢ڢ� B. �ڢۢ� C. �٢ۢ� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣮Ϊ�˴������㴫ͳ�Ļ���ijУ��ί��֯��һ��ȫУ3 000��ѧ���μӵġ�������д�����������������в���ѧ���ijɼ���������50�֣�Ϊ�˸��õ��˽Ȿ�δ����ijɼ��ֲ�����������ȡ������200��ѧ���ijɼ�(�ɼ�xȡ�������ܷ�100��)��Ϊ���������������õ����в�������ͳ��ͼ����
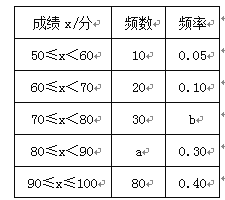
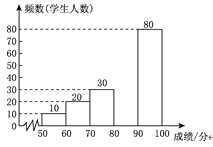
�����������Ϣ������������⣺
(1)a��________��b��________��
(2)�벹ȫƵ���ֲ�ֱ��ͼ��
(3)��α����ɼ�����λ��������________�����Σ�
(4)���ɼ���90������(����90��)��Ϊ���š��ȣ����У�μ���α�����3 000��ѧ���гɼ�Ϊ���š��ȵĴ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
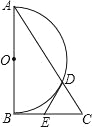
����Ŀ����ͼ��Rt��ABC�У���ABC=90�㣬��ABΪֱ������Բ��O��AC���D����EΪBC���е㣬����DE��
��1����֤��DE�ǰ�Բ��O�����ߣ�
��2������BAC=30�㣬DE=2����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A.3��2a��aB.a2a3��a6
C.��a2��3��a6D.����a��1������a��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
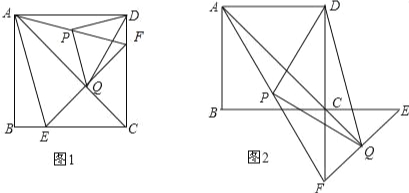
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ��ڱ�BC��CD�ϣ���BE=DF����P��AF���е㣬��Q��ֱ��AC��EF�Ľ��㣬����PQ��PD��
��1����֤��AC��ֱƽ��EF��
��2�����ж���PDQ����״��������֤����
��3����ͼ2��������CEF���ŵ�C��ת180�㣬�����������䣬��2���еĽ��ۻ��������������������֤����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��6������10��+����9����12
��2����32+4������3��������2��3��4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com