
分析 (1)根据实际售价=原定售价-因销售数量增多而降低的价格列出方程,解方程可得;
(2)商场所获得的利润为y与x之间的函数关系式应根据售价的不同分三种情况:0≤x≤10、10<x≤22、x>22,依据总利润=销售数量×每台的利润列出函数关系式,在以上三种情况中分别结合自变量的取值范围求出最大值,比较后可知;
(3)分析(2)中函数的增减性,确定数量的增多,商场所获得的利润反而减少这一情况属于哪一种情形,根据函数性质找到利润最大时的销售单价.
解答 解:(1)设购买x台时,单价恰为3900元,
则4500-50(x-10)=3900,
解得:x=22
故购买22台时,销售单价恰为3900元;
(2)商场所获得的利润为y元与x(台)之间的函数关系式有如下三种情况:
①当0≤x≤10时,y=(4500-3600)x=900x,
②当10<x≤22时,y=x[4500-50(x-10)-3600]=-50x2+1300x,
③当x>22时,y=(3900-3600)x=300x;
商场若要获得最大利润,
①当0≤x≤10时,∵y=900x,y随x增大而增大,
∴当x=10时,y最大且最大值为9000;
②当10<x≤22时,∵y=-50x2+1300x=-50(x-14)2+9800,
∴当x=14时,y最大且最大值为9800;
③当 22<x≤25时∵y=300x,y随x增大而增大,
∴当x=25时,y最大且最大值为7500;
∵7500<9000<9800,
∴一次性购买14台电脑时,利润最大且为9800元
(3)①当0≤x≤10时 y=900x
∵900>0,∴y随x增大而增大
②当10<x≤22时,y=-50x2+1300x=-50(x-14)2+9800,
∵-50<0,
∴当10<x≤14时,y随x增大而增大
当14<x≤22时,y随x增大而减小
∴最低单价应调为4500-50(14-10)=4300元
综上,商场应将最低销售单价调为4300元.
点评 本题主要考查二次函数的实际应用能力,熟知销售问题中关于利润的相等关系是根本,根据售价的不同分不同情况求函数解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
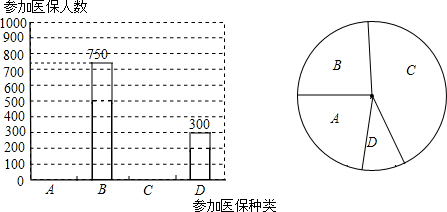
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
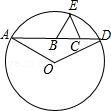 如图,A、B、C、D依次为一直线上4个点,BC=4,△BCE为等边三角形,⊙O过A、D、E三点,且∠AOD=120°.设AB=x,CD=y,则y与x的函数关系式为y=$\frac{16}{x}$.
如图,A、B、C、D依次为一直线上4个点,BC=4,△BCE为等边三角形,⊙O过A、D、E三点,且∠AOD=120°.设AB=x,CD=y,则y与x的函数关系式为y=$\frac{16}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
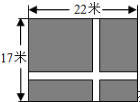 如图,在一块长为22m,宽为17m的矩形地面内,要修筑两条同样宽且互相垂直的道路(两条道路分别与矩形的一条边平行),余下的铺上草坪,要使草坪的面积达到300m2.设道路的宽为x m,根据题意列方程(20-x)(32-x)=300.
如图,在一块长为22m,宽为17m的矩形地面内,要修筑两条同样宽且互相垂直的道路(两条道路分别与矩形的一条边平行),余下的铺上草坪,要使草坪的面积达到300m2.设道路的宽为x m,根据题意列方程(20-x)(32-x)=300.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
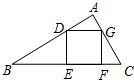 如图,△ABC中∠BAC=90°,正方形DEFG内接于△ABC,且△BDE、△CFG的面积分别为4、1,则△ADG的面积是$\frac{4}{5}$.
如图,△ABC中∠BAC=90°,正方形DEFG内接于△ABC,且△BDE、△CFG的面积分别为4、1,则△ADG的面积是$\frac{4}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com