
【题目】在Rt△ACB中,C为直角顶点,∠ABC=25°,O为斜边AB的中点,将OA绕着点O逆时针旋转α(0°<α<180°)到OP.当△BCP为等腰三角形时,α的度数为________.
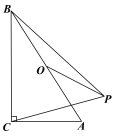
【答案】50°或80°或65°
【解析】
如图1,连接AP,根据直角三角形的判定和性质得到∠APB=90°,当BC=BP时,得到∠BCP=∠BPC,推出AB垂直平分PC,求得∠ABP=∠ABC=25°,于是得到θ=2×25°=50°,当BC=PC时,如图2,连接CO并延长交PB于H,根据线段垂直平分线的性质得到CH垂直平分PB,求得∠CHB=90°,根据等腰三角形的性质得到θ=2×40°=80°,当PB=PC时,如图3,连接PO并延长交BC于G,连接OC,推出PG垂直平分BC,得到∠BGO=90°,根据三角形的内角和得到θ=∠BOG=65°.
∵△BCP恰为轴对称图形,
∴△BCP是等腰三角形,
如图1,连接AP,

∵O为斜边中点,OP=OA,
∴BO=OP=OA,
∴∠APB=90°,
当BC=BP时,
∴∠BCP=∠BPC,
∴∠BCP+∠ACP=∠BPC+∠APC=90°,
∴∠ACP=∠APC,
∴AC=AP,
∴AB垂直平分PC,
∴∠ABP=∠ABC=25°,
∴θ=2×25°=50°,
当BC=PC时,如图2,连接CO并延长交PB于H,

∵BC=CP,BO=PO,
∴CH垂直平分PB,
∴∠CHB=90°,
∵OB=OC,
∴∠BCH=∠ABC=25°,
∴∠CBH=65°,
∴∠OBH=40°,
∴θ=2×40°=80°,
当PB=PC时,如图3,连接PO并延长交BC于G,连接OC,

∵∠ACB=90°,O为斜边中点,
∴OB=OC,
∴PG垂直平分BC,
∴∠BGO=90°,
∵∠ABC=25°,
∴θ=∠BOG=65°,
综上所述:当△BCP恰为轴对称图形时,θ的值为50°或65°或80°,
故答案为:50°或65°或80°.


科目:初中数学 来源: 题型:
【题目】如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=45°,点P在∠AOB的内部.P′与P关于OA对称,P"与P关于OB对称,则O、P′、P"三点所构成的三角形是( )

A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点N(0,6),点M在x轴负半轴上,ON=3OM,A为线段MN上一点,AB⊥x轴,垂足为点B,AC⊥y轴,垂足为点C.
(1)直接写出点M的坐标为 ;
(2)求直线MN的函数解析式;
(3)若点A的横坐标为﹣1,将直线MN平移过点C,求平移后的直线解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图放置的△OAB1 , △B1A1B2 , △B2A2B3 , …都是边长为2的等边三角形,点A在y轴上,点O,B1 , B2 , B3…都在直线l上,则点B2017的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个数能否被99整除是从这个数的末位开始,两位一段,看看这些数段的和能否被99整除.像这样能够被99整除的数,我们称之为“长久数”.例如542718,因为18+27+54=99,所以542718能够被99整除;又例如25146,因为46+51+2=99,所以25146能够被99整除.
(1)若 ![]() 这个三位数是“长久数”,求a的值;
这个三位数是“长久数”,求a的值;
(2)在(1)中的三位数的首位和个位与十位之间加上和为9的两个数字,让其成为一个五位数,该五位数仍是“长久数”,求这个五位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD与AB,CD交于A,D两点,EC,BF与AB,CD交于E,C,B,F,且∠1=∠2,∠B=∠C,

(1)说明CE∥BF.
(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校办工厂现在年产值是15万元,计划以后每年增加2万元.
(1)写出年产值![]() (万元)与年数
(万元)与年数![]() 之间的关系式.
之间的关系式.
(2)用表格表示当![]() 从0变化到6(每次增加1)
从0变化到6(每次增加1)![]() 的对应值.
的对应值.
(3)求5年后的年产值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B的路径运动,且速度为每秒1cm,设出发的时间为t秒.问t为何值时,△BCP为等腰三角形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com