分析 根据平行四边形的性质：平行四边形两组对边分别相等且平行，故①说法正确；根据平行四边形的判定：一组对边平行且相等的四边形是平行四边形可得②说法错误；根据菱形的性质：菱形对角线互相垂直可得③正确；根据对角线互相垂直的平行四边形是菱形可得④错误．
解答 解：①平行四边形的一组对边平行且另一组对边相等，说法正确；
②一组对边平行且另一组对边相等的四边形是平行四边形，说法错误；
③菱形的对角线互相垂直，说法正确；
④对角线互相垂直的四边形是菱形，说法错误；
正确的说法是①③，
故答案为：①③．
点评 此题主要考查了平行四边形的性质和判定，以及菱形的性质和判定，关键是掌握平行四边形的性质和判定定理，菱形的性质和判定定理．
科目：初中数学 来源： 题型：选择题
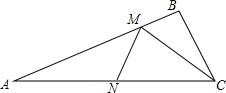如图：△ABC中，AC=6，∠BAC=22.5°，点M、N分别是射线AB和AC上动点，则CM+MN的最小值是（ ）| A． | 2$\sqrt{2}$ | B． | 2$\sqrt{3}$ | C． | 3$\sqrt{2}$ | D． | 3 |
查看答案和解析>>
科目：初中数学 来源： 题型：选择题
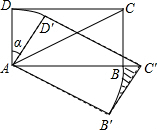如图，在矩形ABCD中，AB=$\sqrt{3}$，AD=1，把该矩形绕点A顺时针旋转α度得矩形AB′C′D′，点C′落在AB的延长线上，则图中阴影部分的面积是（ ）| A． | $\frac{\sqrt{3}}{2}$$-\frac{π}{4}$ | B． | $\frac{\sqrt{3}}{2}-\frac{π}{12}$ | C． | $\frac{\sqrt{3}}{2}-\frac{π}{2}$ | D． | $\frac{\sqrt{3}}{2}-\frac{π}{6}$ |
查看答案和解析>>
科目：初中数学 来源： 题型：选择题
如图，在?ABCD中，E是AD上一点，连接CE并延长交BA的延长线于点F，则下列结论中错误的是（ ）| A． | $\frac{AF}{AB}$=$\frac{AE}{DE}$ | B． | $\frac{AF}{CD}$=$\frac{AE}{BC}$ | C． | $\frac{AF}{AB}=\frac{EF}{CE}$ | D． | $\frac{DE}{AE}=\frac{CE}{EF}$ |
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，将?ABCD的边AB延长至点E，使AB=BE，连接BD、DE、EC，DE交BC于点O．查看答案和解析>>
科目：初中数学 来源： 题型：解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
如图，在菱形ABCD中，已知DE⊥AB，AE：AD=3：5，BE=2，则菱形ABCD的面积是20．