
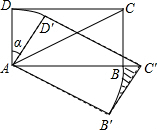
 如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )
如图,在矩形ABCD中,AB=$\sqrt{3}$,AD=1,把该矩形绕点A顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是( )| A. | $\frac{\sqrt{3}}{2}$$-\frac{π}{4}$ | B. | $\frac{\sqrt{3}}{2}-\frac{π}{12}$ | C. | $\frac{\sqrt{3}}{2}-\frac{π}{2}$ | D. | $\frac{\sqrt{3}}{2}-\frac{π}{6}$ |
分析 首先根据题意利用锐角三角函数关系得出旋转角的度数,进而求出S△AB′C′,S扇形BAB′,即可得出阴影部分面积.
解答 解:∵在矩形ABCD中,AB=$\sqrt{3}$,AD=1
∴tan∠CAB=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,AB=CD=$\sqrt{3}$,AD=BC=1,
∴∠CAB=30°,
∴∠BAB′=30°,
∴S△AB′C′=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
S扇形BAB′=$\frac{30π×(\sqrt{3})^{2}}{360}$=$\frac{π}{4}$,
S阴影=S△AB′C′-S扇形BAB′=$\frac{\sqrt{3}}{2}-\frac{π}{4}$.
故选:A.
点评 此题主要考查了矩形的性质以及旋转的性质以及扇形面积公式等知识,得出旋转角的度数是解题关键.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com