
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§÷±œΏ![]() ΫΜ
ΫΜ![]() ÷α”ΎΒψAΘ§ΫΜ
÷α”ΎΒψAΘ§ΫΜ![]() ÷α”ΎΒψCΘ®0,4Θ©.≈ΉΈοœΏ
÷α”ΎΒψCΘ®0,4Θ©.≈ΉΈοœΏ![]()
Ψ≠ΙΐΒψAΘ§ΫΜ![]() ÷α”ΎΒψBΘ®0Θ§-2Θ©.ΒψPΈΣ≈ΉΈοœΏ…œ“ΜΗωΕ·ΒψΘ§Ψ≠ΙΐΒψPΉς
÷α”ΎΒψBΘ®0Θ§-2Θ©.ΒψPΈΣ≈ΉΈοœΏ…œ“ΜΗωΕ·ΒψΘ§Ψ≠ΙΐΒψPΉς![]() ÷αΒΡ¥ΙœΏPDΘ§ΙΐΒψBΉςBDΓΆPD”ΎΒψDΘ§Ν§Ϋ”PBΘ§…ηΒψPΒΡΚαΉχ±ξΈΣ
÷αΒΡ¥ΙœΏPDΘ§ΙΐΒψBΉςBDΓΆPD”ΎΒψDΘ§Ν§Ϋ”PBΘ§…ηΒψPΒΡΚαΉχ±ξΈΣ![]() .
.
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Β±ΓςBDPΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ ±Θ§«σœΏΕΈPDΒΡ≥ΛΘΜ
Θ®3Θ©»γΆΦ2Θ§ΫΪΓςBDP»ΤΒψBΡφ ±’κ–ΐΉΣΘ§ΒΟΒΫΓςBDΓδPΓδΘ§«“–ΐΉΣΫ«ΓœPBPΓδ=ΓœOACΘ§Β±ΒψPΒΡΕ‘”ΠΒψPΓδ¬δ‘ΎΉχ±ξ÷α…œ ±Θ§«κ÷±Ϋ”–¥≥ωΒψPΒΡΉχ±ξ.



ΓΨ¥πΑΗΓΩ(1)![]() ΘΜΘ®2Θ©Β±ΓςBPDΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ ±Θ§PDΒΡ≥ΛΈΣ
ΘΜΘ®2Θ©Β±ΓςBPDΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ ±Θ§PDΒΡ≥ΛΈΣ![]() .(3)
.(3)![]() ,
,![]() ,
,![]() .
.
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚ(1)œ»«σΒΟΒψAΒΡΉχ±ξΘ§‘Όάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≈ΉΈοœΏΒΡΫβΈω ΫΦ¥Ω…ΘΜΘ®2Θ©…ηΒψPΒΡΚαΉχ±ξΈΣ![]() ,Ω…ΒΟP(mΘ§
,Ω…ΒΟP(mΘ§![]() )Θ§D(mΘ§-2)Θ§»τΓςBPDΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρPD=BD.Ζ÷ΝΫ÷÷«ιΩωΘΚΔΌΒ±ΒψP‘Ύ÷±œΏBDΒΡ…œΖΫ ±Θ§PD=
)Θ§D(mΘ§-2)Θ§»τΓςBPDΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρPD=BD.Ζ÷ΝΫ÷÷«ιΩωΘΚΔΌΒ±ΒψP‘Ύ÷±œΏBDΒΡ…œΖΫ ±Θ§PD=![]() ,‘ΌΖ÷ΒψP‘Ύy÷αΒΡΉσ≤ύΚΆ”“≤ύΝΫ÷÷«ιΩωΘ§Ν–ΖΫ≥Χ«σΫβΦ¥Ω…ΘΜΔΎΒ±ΒψP‘Ύ÷±œΏBDΒΡœ¬ΖΫ ±Θ§mΘΨ0Θ§BD=mΘ§PD=
,‘ΌΖ÷ΒψP‘Ύy÷αΒΡΉσ≤ύΚΆ”“≤ύΝΫ÷÷«ιΩωΘ§Ν–ΖΫ≥Χ«σΫβΦ¥Ω…ΘΜΔΎΒ±ΒψP‘Ύ÷±œΏBDΒΡœ¬ΖΫ ±Θ§mΘΨ0Θ§BD=mΘ§PD=![]() ,Ν–ΖΫ≥Χ«σΫβΦ¥Ω…ΘΜΘ®3Θ©ΓΏΓœPBP/=ΓœOAC,OA=3,OC=4ΘΜΓύAC=5Θ§ΓύsinΓœPBP/=
,Ν–ΖΫ≥Χ«σΫβΦ¥Ω…ΘΜΘ®3Θ©ΓΏΓœPBP/=ΓœOAC,OA=3,OC=4ΘΜΓύAC=5Θ§ΓύsinΓœPBP/=![]() Θ§cosΓœPBP/=
Θ§cosΓœPBP/=![]() Θ§ΔΌΒ±ΒψP/¬δ‘Ύx÷α…œ ±Θ§ΙΐΒψD/ΉςD/NΓΆx÷α”ΎNΘ§ΫΜBD”ΎΒψMΘ§ΓœDBD/=ΓœND/P/=ΓœPBP/,»γΆΦ1Θ§ND/-MD/=2,Φ¥
Θ§ΔΌΒ±ΒψP/¬δ‘Ύx÷α…œ ±Θ§ΙΐΒψD/ΉςD/NΓΆx÷α”ΎNΘ§ΫΜBD”ΎΒψMΘ§ΓœDBD/=ΓœND/P/=ΓœPBP/,»γΆΦ1Θ§ND/-MD/=2,Φ¥![]() ΓΝ(
ΓΝ(![]() m2-
m2-![]() m)-Θ®-
m)-Θ®-![]() mΘ©=2ΘΜ»γΆΦ2Θ§ND/-MD/=2Θ§Φ¥
mΘ©=2ΘΜ»γΆΦ2Θ§ND/-MD/=2Θ§Φ¥![]() ΓΝ(
ΓΝ(![]() m2-
m2-![]() m)-Θ®-
m)-Θ®-![]() mΘ©=2ΫβΒΟΘΚPΘ®Θ≠
mΘ©=2ΫβΒΟΘΚPΘ®Θ≠![]() Θ§
Θ§![]() Θ©ΜρPΘ®
Θ©ΜρPΘ®![]() Θ§
Θ§![]() Θ©ΘΜΔΎΒ±ΒψP/¬δ‘Ύy÷α…œ ±Θ§
Θ©ΘΜΔΎΒ±ΒψP/¬δ‘Ύy÷α…œ ±Θ§
»γΆΦ3Θ§ΙΐΒψD/ΉςD/MΓΆx÷αΫΜBD”ΎΒψMΘ§ΙΐΒψP/ΉςP/NΓΆy÷αΘ§ΫΜMD/ΒΡ―”≥ΛœΏ”ΎΒψNΘ§ΓœDBD/=ΓœND/P/=ΓœPBP/,ΓΏPN=BM,Φ¥ ![]() ΓΝ(
ΓΝ(![]() m2-
m2-![]() m)=
m)= ![]() mΓύPΘ®
mΓύPΘ®![]() Θ§
Θ§![]() Θ©
Θ©

‘ΧβΫβΈωΘΚ(1)”…÷±œΏ![]() ΙΐΒψCΘ®0,4Θ©Θ§ΒΟn=4Θ§Γύ
ΙΐΒψCΘ®0,4Θ©Θ§ΒΟn=4Θ§Γύ![]() .
.
Β±y=0 ±Θ§![]() Θ§ΫβΒΟx=3Θ§ΓύAΘ®3,0Θ©.
Θ§ΫβΒΟx=3Θ§ΓύAΘ®3,0Θ©.
ΓΏ≈ΉΈοœΏ![]() Ψ≠ΙΐΒψAΘ®3,0Θ©Θ§BΘ®0Θ§-2Θ©Θ§
Ψ≠ΙΐΒψAΘ®3,0Θ©Θ§BΘ®0Θ§-2Θ©Θ§
Γύ Θ§ΫβΒΟ
Θ§ΫβΒΟ
Γύ![]() .
.
(2)…ηΒψPΒΡΚαΉχ±ξΈΣ![]() ,ΓύP(mΘ§
,ΓύP(mΘ§![]() )Θ§D(mΘ§-2).
)ȧD(mȧ-2).
»τΓςBPDΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρPD=BD.
ΔΌΒ±ΒψP‘Ύ÷±œΏBDΒΡ…œΖΫ ±Θ§PD=![]() ,
,
(I)»τΒψP‘Ύy÷αΒΡΉσ≤ύΘ§‘ρmΘΦ0Θ§BD=-mΘ§
Γύ![]() Θ§
Θ§
ΫβΒΟ![]() Θ®…α»ΞΘ©.
Θ®…α»ΞΘ©.
(II)»τΒψP‘Ύy÷αΒΡ”“≤ύΘ§‘ρmΘΨ0Θ§BD=mΘ§
Γύ![]() Θ§
Θ§
ΫβΒΟ![]() .
.
ΔΎΒ±ΒψP‘Ύ÷±œΏBDΒΡœ¬ΖΫ ±Θ§mΘΨ0Θ§BD=mΘ§PD=![]() ,
,
Γύ![]() Θ§
Θ§
ΫβΒΟ![]() .
.
Ήέ…œm=![]() .
.
Φ¥Β±ΓςBPDΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ ±Θ§PDΒΡ≥ΛΈΣ![]() .
.
(3)![]() ,
,![]() ,
,![]() .
.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΙΊ”ΎxΒΡΖΫ≥Χx2©¹4x+3©¹aΘΫ0”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ°
Θ®1Θ©«σaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©Β±a»Γ¬ζΉψΧθΦΰΒΡΉν–Γ’ϊ ΐ÷Β ±Θ§«σΖΫ≥ΧΒΡΫβΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβ―ß…ζΒΡ“’ θΧΊ≥ΛΖΔ’Ι«ιΩωΘ§Ρ≥–Θ“τά÷ΉιΨωΕ®Έß»Τ‘ΎΓΑΈηΒΗΓΔά÷ΤςΓΔ…υά÷ΓΔœΖ«ζΓΔΤδΥϋΜνΕ·Γ±œνΡΩ÷–Θ§ΡψΉνœ≤ΜΕΡΡ“ΜœνΜνΕ·Θ®ΟΩ»Υ÷Μœό“ΜœνΘ©ΒΡΈ ΧβΘ§‘Ύ»Ϊ–ΘΖΕΈßΡΎΥφΜζ≥ι»Γ≤ΩΖ÷―ß…ζΫχ––Έ ΨμΒς≤ιΘ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΓΘ
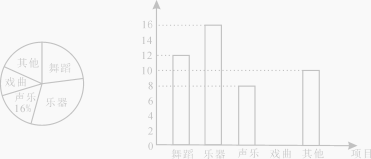
«κΡψΗυΨίΆ≥ΦΤΆΦΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©‘Ύ’β¥ΈΒς≤ι÷–Θ§“ΜΙ≤≥ι≤ιΝΥ Οϊ―ß…ζΓΘΤδ÷–œ≤ΜΕΓΑΈηΒΗΓ±ΜνΕ·œνΡΩΒΡ»Υ ΐ’Φ≥ι≤ιΉή»Υ ΐΒΡΑΌΖ÷±»ΈΣ ΓΘ…»–ΈΆ≥ΦΤΆΦ÷–œ≤ΜΕΓΑœΖ«ζΓ±≤ΩΖ÷…»–ΈΒΡ‘≤–ΡΫ«ΈΣ Ε»ΓΘ
Θ®2Θ©«κΡψ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΓΘ
Θ®3Θ©»τ‘ΎΓΑΈηΒΗΓΔά÷ΤςΓΔ…υά÷ΓΔœΖ«ζΓ±œνΡΩ÷–»Έ―ΓΝΫœν≥…ΝΔΩΈΆβ–Υ»Λ–ΓΉιΘ§«κ”ΟΝ–±μΜρΜ≠ ςΉ¥ΆΦΒΡΖΫΖ®«σ«ΓΚΟ―Γ÷–ΓΑΈηΒΗΓΔ…υά÷Γ±’βΝΫœνΒΡΗ≈¬ ΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ0ΘΦaΘΦ2Θ§‘ρΒψPΘ®aΘ§a-2Θ©‘ΎΡΡΗωœσœόΘ® Θ©
A.ΒΎ“Μœσœό
B.ΒΎΕΰœσœό
C.ΒΎ»ΐœσœό
D.ΒΎΥΡœσœό
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν––π ω’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
A. ΤΫΖ÷œ“ΒΡ÷±ΨΕ±Ί¥Ι÷±”Ύœ“ B. »ΐΫ«–ΈΒΡΆβ–ΡΒΫ»ΐ±ΏΒΡΨύάκœύΒ»
C. »ΐΫ«–ΈΒΡΡΎ–Ρ «»ΐΧθΫ«ΤΫΖ÷œΏΒΡΫΜΒψ D. œύΒ»ΒΡ‘≤÷ήΫ«ΥυΕ‘ΒΡΜΓœύΒ»
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ
»γΆΦΘ§≈ΉΈοœΏL: ![]() Θ®≥Θ ΐt>0Θ©”κx÷α¥”ΉσΒΫ”“ΒΡΫΜΒψΈΣBΘ§AΘ§ΙΐœΏΕΈOAΒΡ÷–ΒψMΉςMPΓΆx÷αΘ§ΫΜΥΪ«ζœΏ
Θ®≥Θ ΐt>0Θ©”κx÷α¥”ΉσΒΫ”“ΒΡΫΜΒψΈΣBΘ§AΘ§ΙΐœΏΕΈOAΒΡ÷–ΒψMΉςMPΓΆx÷αΘ§ΫΜΥΪ«ζœΏ![]() ”ΎΒψPΘ§«“OAΓΛMP=12.
”ΎΒψPΘ§«“OAΓΛMP=12.
Θ®1Θ©«σk÷ΒΘΜ
Θ®2Θ©Β±t=1 ±Θ§«σAB≥ΛΘ§≤Δ«σ÷±œΏMP”κLΕ‘≥Τ÷α÷°ΦδΒΡΨύάκΘΜ
Θ®3Θ©Α―L‘Ύ÷±œΏMPΉσ≤ύ≤ΩΖ÷ΒΡΆΦœσΘ®Κ§”κ÷±œΏMPΒΡΫΜΒψΘ©Φ«ΈΣGΘ§”Οt±μ ΨΆΦœσGΉνΗΏΒψΒΡΉχ±ξΘΜ
Θ®4Θ©…ηL”κΥΪ«ζœΏ”–ΗωΫΜΒψΒΡΚαΉχ±ξΈΣx0Θ§«“¬ζΉψ4Γήx0Γή6Θ§Ά®ΙΐLΈΜ÷ΟΥφt±δΜ·ΒΡΙΐ≥ΧΘ§÷±Ϋ”–¥≥ωtΒΡ»Γ÷ΒΖΕΈß.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒψP(Θ≠2Θ§3)ΙΊ”Ύx÷αΒΡΕ‘≥ΤΒψΒΡΉχ±ξΈΣΘ® Θ©
A.(2,3)B.(Θ≠2Θ§Θ≠3)C.(2Θ§Θ≠3)D.(Θ≠3,2)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏy=ax2+2x+6Θ®aΓΌ0Θ©ΫΜx÷α”κAΘ§BΝΫΒψΘ®ΒψA‘ΎΒψBΉσ≤ύΘ©Θ§ΫΪ÷±≥ΏWXYZ”κx÷αΗΚΖΫœρ≥…45ΓψΖ≈÷ΟΘ§±ΏWZΨ≠Ιΐ≈ΉΈοœΏ…œΒΡΒψCΘ®4Θ§mΘ©Θ§”κ≈ΉΈοœΏΒΡΝμ“ΜΫΜΒψΈΣΒψDΘ§÷±≥Ώ±Μx÷αΫΊΒΟΒΡœΏΕΈEF=2Θ§«“ΓςCEFΒΡΟφΜΐΈΣ6Θ°
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΧΫΨΩΘΚ‘Ύ÷±œΏAC…œΖΫΒΡ≈ΉΈοœΏ…œ «Ζώ¥φ‘Ύ“ΜΒψPΘ§ ΙΒΟΓςACPΒΡΟφΜΐΉν¥σΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΟφΜΐΒΡΉν¥σ÷ΒΦΑ¥Υ ±ΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
Θ®3Θ©ΫΪ÷±≥Ώ“‘ΟΩΟκ2ΗωΒΞΈΜΒΡΥΌΕ»―Ίx÷αœρΉσΤΫ“ΤΘ§…ηΤΫ“ΤΒΡ ±ΦδΈΣtΟκΘ§ΤΫ“ΤΚσΒΡ÷±≥ΏΈΣWΓδXΓδYΓδZΓδΘ§Τδ÷–±ΏXΓδYΓδΥυ‘ΎΒΡ÷±œΏ”κx÷αΫΜ”ΎΒψMΘ§”κ≈ΉΈοœΏΒΡΤδ÷–“ΜΗωΫΜΒψΈΣΒψNΘ§«κ÷±Ϋ”–¥≥ωΒ±tΈΣΚΈ÷Β ±Θ§Ω… ΙΒΟ“‘CΓΔDΓΔMΓΔNΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΨίΆ≥ΦΤΘ§2015ΡξΙζ«λΤΎΦδΘ§ΈόΈΐΝι…ΫΖγΨΑ«χΡ≥“ΜΧλΫ”¥ΐ”ΈΩΆΒΡ»Υ ΐΈΣ19800»Υ¥ΈΘ§ΫΪ’βΗω ΐΉ÷ΨΪ»ΖΒΫ«ßΈΜΘ§≤Δ”ΟΩΤ―ßΦ« ΐΖ®±μ ΨΈΣ Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com