
【题目】已知:如图,△ABC∽△ADE , AE:EC=5:3,BC=6cm,∠A=40°,∠C=45°.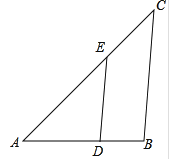
(1)求∠ADE的大小;
(2)求DE的长.
【答案】
(1)
解答:在△ABC中,∠A=40°,∠C=45°,
∴∠ABC=180°-40°-45°=95°;
又∵△ABC∽△ADE,
∴∠ADE=∠ABC(相似三角形的对应角相等),
∴∠ADE =95°;
(2)
解答:∵AE:EC=5:3,
∴AE:AC=5:8;
又∵△ABC∽△ADE,BC=6cm,
∴ ![]() ,即
,即 ![]()
∴DE= ![]() cm.
cm.
【解析】先由三角形的内角和是180°求得∠ABC=95°;再由相似三角形的对应角相等得出∠ADE=∠ABC , 最后由等量代换求得∠ADE的大小;由AE:EC=5:3求得AE:AC=5:8,再根据相似三角形的对应边成比例求得DE的长度.此题主要考查了相似三角形的性质:相似三角形的对应角相等,对应边成比例.
【考点精析】认真审题,首先需要了解相似三角形的性质(对应角相等,对应边成比例的两个三角形叫做相似三角形).


科目:初中数学 来源: 题型:
【题目】当x>0时,反比例函数 ![]() ( )
( )
A.图象在第四象限,y随x的增大而增大
B.图象在第三象限,y随x的增大而增大
C.图象在第二象限,y随x的增大而减小
D.图象在第一象限,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
(1)求证:PE=PD;
(2)连接DE,试判断∠PED的度数,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空: a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.
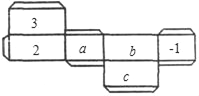
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CA⊥BA
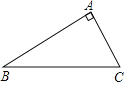
(1)画图:①延长BA到D,使AD=BA,连接CD;
②过点A画AE∥BC,AE与CD相交于点E;
③过点B画BF⊥CD,交DC的延长线于点F.
思考:图中有______条线段,它们的长度表示点到直线的距离;
(2)度量:
①你度量的哪些量?______;
②通过度量你发现:______.(写一条发现即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组从A地出发,在东西方向的公路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶,纪录如下(单位:km)
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 |
﹣4 | +7 | ﹣9 | +8 | +6 | ﹣5 | ﹣2 |
则收工时距A地多远?在第几次纪录时距A地最远?
A. 2千米 第1次 B. 1千米 第2次
C. 2千米 第4次 D. 1千米 第5次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下: 甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )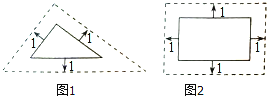
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地,乙车比甲车晚出发2小时(从甲车出发时开始计时),图中折线OABC、线段DE分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图像线段AB表示甲出发不足2小时因故停车检修),请根据图像所提供的信息,解决如下问题:
(1)求乙车所行路程y与时间x的函数关系式;
(2)求两车在途中第二次相遇时,它们距出发地的路程;
(3)乙车出发多长时间,两车在途中第一次相遇?(写出解题过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com