
分析 (1)根据若两车合作,各运12趟才能完成,需支付运费共4800元,乙车每趟运费比甲车少200元,列出方程组,即可解答;
(2)设单独租用甲车运完此堆垃圾,需运a趟,由题意列出分式方程,即可解答;
(3)①根据$\frac{x}{18}$+$\frac{y}{36}$=1即可解答;
②根据总运费=甲的运费+乙的运费,列出函数关系式,利用一次函数的性质,即可解答;
③根据甲车每趟的运费打7折,乙车每趟的运费打9折,列出函数关系式,再根据x≥10且y≥10,确定x的值,即可解答.
解答 解:(1)设甲、乙两车每趟的运费分别为m元、n元,
由题意得$\left\{\begin{array}{l}{m-n=200}\\{12(m+n)=4800}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=300}\\{n=100}\end{array}\right.$.
答:甲、乙两车每趟的运费分别为300元、100元.
(2)设单独租用甲车运完此堆垃圾,需运a趟,由题意得
12($\frac{1}{a}$+$\frac{1}{2a}$)=1,
解得 a=18,
经检验a=18是原方程的解.
答:单独租用甲车运完此堆垃圾,需运18趟.
(3)①∵$\frac{x}{18}$+$\frac{y}{36}$=1,
∴y=36-2x;
②w=300x+100y=300x+100(36-2x),
=100x+3600,(0<x<18,且x为正整数),
∵100>0,
∴y随x的增大而增大,
∴当x=1时,有最小值,w的最小值3700元.
③w=300×0.7x+100×0.9y=300×0.7x+100×0.9(36-2x)=30x+3240,
∵x≥10且y≥10,
∴10≤x≤13,且x为正整数,
w的最小值3540元.
点评 本题考查了一次函数的应用,解决本题的关键是根据题意列出函数关系式.


科目:初中数学 来源: 题型:选择题
| A. | ac>bc | B. | $\frac{1}{a}$$<\frac{1}{b}$ | C. | |a|>|b| | D. | ac2≥bc2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
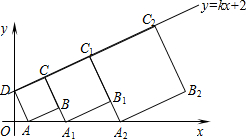 在平面直角坐标系中,直线y=kx+2与y轴交于点D,点A的坐标为(1,0),以AD为边作正方形ABCD.点C在直线y=kx+2上,延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第1个正方形(即正方形ABCD)的面积为5.第2014个正方形的面积为5×$(\frac{9}{4})^{2014}$.
在平面直角坐标系中,直线y=kx+2与y轴交于点D,点A的坐标为(1,0),以AD为边作正方形ABCD.点C在直线y=kx+2上,延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第1个正方形(即正方形ABCD)的面积为5.第2014个正方形的面积为5×$(\frac{9}{4})^{2014}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com