
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连结BE交AC于F,连结FD,若∠BFA=90°,则下列四对三角形:①△BEA与△ACD②△FED与△DEB③△CFD与△ABG④△ADF与△CFB中相似的为( )

A. ①④B. ①②C. ②③④D. ①②③
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD各个顶点的坐标分别为A(﹣2,8),B(﹣11,6),C(﹣14,0),D(0,0).
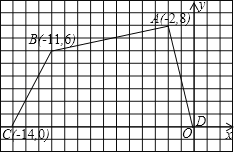
(1)求这个四边形的面积;
(2)如果把四边形ABCD各个顶点的纵坐标保持不变,横坐标增加4,所得的四边形的面积又是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
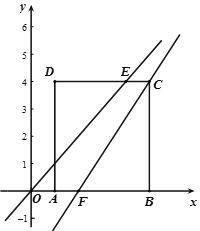
【题目】将边长为4的正方形ABCD置于平面直角坐标系中,使AB边落在x轴的正半轴上且A点的坐标是![]() ,直线y=x与线段CD交于点E.
,直线y=x与线段CD交于点E.
(1)直线![]() 经过点C且与
经过点C且与![]() 轴交于点F.求四边形AFCD的面积.
轴交于点F.求四边形AFCD的面积.
(2)若直线![]() 经过点E和点F,求直线
经过点E和点F,求直线![]() 的解析式.
的解析式.
(3)若直线![]() 经过点
经过点![]() 且与直线
且与直线![]() 平行,将(2)中直线
平行,将(2)中直线![]() 沿着
沿着![]() 轴向上平移1个单位得到直线
轴向上平移1个单位得到直线![]() ,直线
,直线![]() 交
交![]() 轴于点M,交直线
轴于点M,交直线![]() 于点N,求
于点N,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B是切点,点C是劣弧AB上的一点,若∠P=40°,则∠ACB等于( )
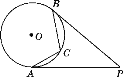
A. 80° B. 110° C. 120° D. 140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在![]() 处,
处,![]() 交AD于点E.
交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若![]() ,
,![]() ,求△BDE的面积.
,求△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
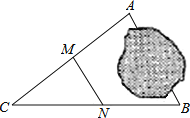
A. AB=24m B. MN∥AB
C. △CMN∽△CAB D. CM:MA=1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为10,点E、F、G、H分别在AB、BC、CD、DA上,且满足AE∶BF∶CG∶DH=1∶2∶3∶4. 问当AE长为多少时,四边形EFGH的面积最小?并求出这个最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com