
����Ŀ��ij��������������A��B��C��ͬһ��·�ϣ��ס��������οʹӾ���A�������ײ��е�����C�����ȳ˾����۹������B����B��ͣ��һ��ʱ����ٲ��е�����C���ס�������ͬʱ���ᄚ��C���ס������˾ྰ��A��·��y(��)��׳�����ʱ��x(��)֮��ĺ���ͼ����ͼ��ʾ��
(1)�ײ��е��ٶ�Ϊ_____��/�֣��Ҳ���ʱ���ٶ�Ϊ_____��/�֣�
(2)���ҳ˾����۹ʱy��x֮��ĺ�����ϵʽ��
(3)�ʼ׳����ʱ��������;����������ֱ��д�������
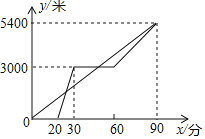
���𰸡�(1)60��80��(2)y��300x��6000(20��x��30)��(3)�׳���25���Ӻ�50��������������;��������
��������
(1)��ͼ�����Ӧ��·�̺�ʱ�䣬����·�̳���ʱ����ٶȣ�
(2)���ҳ˾����۹ʱy��x֮��ĺ�����ϵʽΪy��kx+b(k��0)����(20��0)��(30��3000)���룬���k��b��ֵ�ٴ��ؼ��ɣ�
(3)������ĺ�������ʽ���ٽ������ҳ˹۹ʱ�Ľ���ʽ�����õ�һ������ʱ�䣻�ڼĽ���ʽ�У���y��3000����õڶ�������ʱ�䣮
(1)�ײ��е��ٶ�Ϊ��5400��90��60(��/��)��
�Ҳ��е��ٶ�Ϊ��(5400��3000)��(90��60)��80(��/��)��
�ʴ�Ϊ��60��80��
(2)�⣺�������⣬���ҳ˾����۹ʱy��x֮��ĺ�����ϵʽΪy��kx+b(k��0)����(20��0)��(30��3000)����ã�
![]() ��ã�
��ã�![]() ��
��
���ҳ˾����۹ʱy��x֮��ĺ�����ϵʽΪy��300x��6000(20��x��30)
(3)��ĺ�������ʽΪ��y��kx����(90��5400)�����k��60��
��y��60x��
��![]() ��x��25�����׳���25�������ҵ�һ��������
��x��25�����׳���25�������ҵ�һ��������
��y��60x�У���y��3000�ã�x��50����ʱ�����ҵڶ���������
�׳���25���Ӻ�50��������������;��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
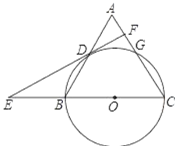
����Ŀ����ͼ������ABC�У�CA=CB=10��AB=12����BCΪֱ����Բ��O��AC�ڵ�G����AB�ڵ�D������D����O�����ߣ���CB���ӳ����ڵ�E����AC�ڵ�F�������н��ۣ���DF��AC����DO=DB����cos��E=![]() ����ȷ����__.
����ȷ����__.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����幺��ij����Ʊ��Ʊ�������ij��λ��Ҫ��֯���г�������������Ա�������ù��������������Ϊ���壬ѡ��������ͬ��ʱ��ֱ�Ʊ������������֧����Ʊ��Ϊ1290Ԫ������������ź���һ����Ϊһ�����壬ͬһʱ�乺Ʊ������������֧����Ʊ��Ϊ990Ԫ����ô�ù�˾���������ŵ�����֮��Ϊ��������

A. 20B. 35C. 30D. 40
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ���װ���ĸ��ֱ����1��2��3��4��С�����ǵ���״����С����ȫ��ͬ.С���ȴӿڴ���������Żص�ȡ��һ��С��������Ϊx��С����ʣ��������С�������ȡ��һ��С��������y.
(1)������x��yȷ���ĵ�(x��y)�ں���![]() ͼ���ϵĸ��ʣ�
ͼ���ϵĸ��ʣ�
(2)С�ڡ�С��Լ����һ����Ϸ��������ǣ���x��y����xy>6����С��ʤ����x��y����xy<6,��С��ʤ.�����Ϸ����ƽ��?˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�1������ѧ��ȤС�龭���г����飬������ij����Ʒ�ڵ�x��1��x��90������ۼ����������������Ϣ���±���
ʱ��x���죩 | 1��x��50 | 50��x��90 |
�ۼۣ�Ԫ/���� | x��40 | 90 |
ÿ������������ | 200��2x | |
��֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒ��ÿ������ΪyԪ[
��1�����y��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������4800Ԫ����ֱ��д�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л�������ԴԶ�������л����֣�Ԣ����㣮Ϊ�����л����㴫ͳ�Ļ���ijУ��ί��֯��һ��ȫУ3000��ѧ���μӵ���������д��������Ϊ�˽Ȿ�δ����ijɼ���У��ί�����ȡ������200��ѧ���ijɼ���Ϊ��������ͳ�ƣ��Ƴ����²�������ͳ��ͼ����
Ƶ��Ƶ�ʷֲ���
�ɼ�x���֣� | Ƶ�����ˣ� | Ƶ�� |
50��x��60 | 10 | 0.05 |
60��x��70 | 30 | 0.15 |
70��x��80 | 40 | n |
80��x��90 | m | 0.35 |
90��x��100 | 50 | 0.25 |
����������Ϣ������������⣺
��1��m=�� ����n=�� ����
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����200��ѧ���ɼ�����λ���������� �������Σ�
��4�����ɼ���90�����ϣ�����90�֣�Ϊ�������ȣ�������Ƹ�У�μӱ��α�����3000��ѧ���гɼ����������ȵ�Լ�ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ�����װ�д�С����״��ͬ��3�������2���������dz�ֽ��ȣ�
��1�������������ȡ1�����Ǻ�����ǰ��������� ���¼��������������ȡ1�����Ǻ��������� ���¼���
��2�����������ȡ1����ǡ���Ǻ���ĸ������� ����
��3��ѧУ�����ڼס�������ͬѧ��ѡȡһ����Ϊѧ���������ԣ��ƶ����¹��Ӻ�������ȡ������������ͬɫ����ѡ�ף���������ɫ����ѡ�ң�����Ϊ�������ƽ�������б�������״ͼ������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ���ڵ㣨1��0����ֱ��
���ڵ㣨1��0����ֱ��![]() ���ڵ㣨2��0����ֱ��
���ڵ㣨2��0����ֱ��![]() ���ڵ㣨3��0��������ֱ��
���ڵ㣨3��0��������ֱ��![]() ���ڵ㣨n��0��������
���ڵ㣨n��0��������![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ������
������![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() �����
�����![]() ���������
���������![]() ���ı���
���ı���![]() ���������
���������![]() ���ı���
���ı���![]() ���������
���������![]() �������ı���
�������ı���![]() ���������
���������![]() ����ô
����ô![]() _____________��
_____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
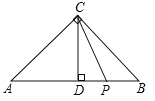
����Ŀ����ͼ���ڡ�ABC�У���ACB=90������A=45����CD��AB�ڵ�D����P���߶�DB�ϣ���AP2-PB2=48�����PCD�����Ϊ____.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com