
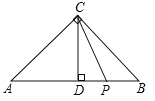
【题目】如图,在△ABC中,∠ACB=90°,∠A=45°,CD⊥AB于点D,点P在线段DB上,若AP2-PB2=48,则△PCD的面积为____.
【答案】6
【解析】
根据等角对等边,可得AC=BC,由等腰三角形的“三线合一”可得AD=BD=![]() AB,利用直角三角形斜边的中线等于斜边的一半,可得CD=
AB,利用直角三角形斜边的中线等于斜边的一半,可得CD=![]() AB,由AP2-PB2=48,利用平方差公式及线段的和差公式将其变形可得CD·PD=12,利用△PCD的面积 =
AB,由AP2-PB2=48,利用平方差公式及线段的和差公式将其变形可得CD·PD=12,利用△PCD的面积 =![]() CD·PD可得.
CD·PD可得.
解:∵ 在△ABC中,∠ACB=90°,∠A=45°,
∴∠B=45°,
∴AC=BC,
∵CD⊥AB,
∴AD=BD=CD=![]() AB,
AB,
∵AP2-PB2=48,
∴(AP+PB)(AP-PB)=48,
∴AB(AD+PD-BD+DP)=48,
∴AB·2PD=48,
∴2CD·2PD=48,
∴CD·PD=12,
∴ △PCD的面积=![]() CD·PD=6.
CD·PD=6.
故答案为:6.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 分别是
分别是![]() 轴上位于原点两侧的两点,点
轴上位于原点两侧的两点,点![]() 在第一象限,直线
在第一象限,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() .
.
(1)求![]() ;
;
(2)求点![]() 的坐标及
的坐标及![]() 的值;
的值;
(3)若![]() ,求直线
,求直线![]() 的函数表达式.
的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
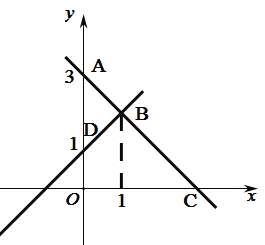
【题目】如图,过点![]() 的直线
的直线![]() 与一次函数
与一次函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的坐标及直线
的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)求直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标;
的坐标;
(3)![]() 为
为![]() 的图象与
的图象与![]() 轴的交点,求四边形
轴的交点,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在
在![]() 的正北方向,
的正北方向,![]() 在
在![]() 的正东方向,且
的正东方向,且![]() .某一时刻,甲车从
.某一时刻,甲车从![]() 出发,以
出发,以![]() 的速度朝正东方向行驶,与此同时,乙车从
的速度朝正东方向行驶,与此同时,乙车从![]() 出发,以
出发,以![]() 的速度朝正北方向行驶.
的速度朝正北方向行驶.![]() 小时后,位于点
小时后,位于点![]() 处的观察员发现甲、乙两车之间的夹角为
处的观察员发现甲、乙两车之间的夹角为![]() ,即
,即![]() ,此时,甲、乙两人相距的距离为( )
,此时,甲、乙两人相距的距离为( )

A. 90km B. 50![]() km C. 20
km C. 20![]() km D. 100km
km D. 100km
查看答案和解析>>
科目:初中数学 来源: 题型:
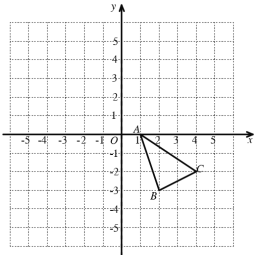
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]()
(1)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,画出
,画出![]() 向左平移3个单位长度后得到的
向左平移3个单位长度后得到的![]() ,
,
(2)如果![]() 上有一点
上有一点![]() 经过上述两次变换,那么对应
经过上述两次变换,那么对应![]() 上的点
上的点![]() 的坐标是______
的坐标是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在![]() 处用高
处用高![]() 米(
米(![]() 米)的测角仪测得旗杆
米)的测角仪测得旗杆![]() 的顶端
的顶端![]() 的仰角为
的仰角为![]() ,再向旗杆方向前进
,再向旗杆方向前进![]() 米到
米到![]() 处,又测得旗杆顶端
处,又测得旗杆顶端![]() 的仰角为
的仰角为![]() ,请求出旗杆
,请求出旗杆![]() 的高度(取
的高度(取![]() ,结果保留整数)
,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 过点
过点![]() 和
和![]() 对于该二次函数有如下说法:
对于该二次函数有如下说法:
①它的图象与![]() 轴有两个公共点;
轴有两个公共点;
②若存在一个正数![]() ,使得当
,使得当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而减小,则
的增大而减小,则![]() ;若存在一个负数
;若存在一个负数![]() ,使得当
,使得当![]() 时,函数值
时,函数值![]() 随
随![]() 的增大而增大,则
的增大而增大,则![]() ;
;
③若将它的图象向左平移![]() 个单位后过原点,则
个单位后过原点,则![]() ;
;
④若当![]() 时的函数值与
时的函数值与![]() 时的函数值相等,则当
时的函数值相等,则当![]() 时的函数值为
时的函数值为![]() .
.
其中正确的说法的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边在右侧作等边△ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )

A. 平行 B. 相交 C. 垂直 D. 平行、相交或垂直
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com