
【题目】团体购买某公园门票,票价如表,某单位现要组织其市场部和生产部的员工游览该公园.如果按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;如果两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元.那么该公司这两个部门的人数之差为( )

A. 20B. 35C. 30D. 40
【答案】C
【解析】
根据990不能被13整除,得两个部门人数之和:a+b≥51,然后结合门票价格和人数之间的关系,建立方程组进行求解即可.
解:∵990不能被13整除,∴两个部门人数之和:a+b≥51,
(1)若51≤a+b≤100,则11 (a+b)=990得:a+b=90,①
由共需支付门票费为1290元可知,11a+13b=1290 ②
解①②得:b=150,a=-60,不符合题意.
(2)若a+b≥100,则9 (a+b)=990,得 a+b=110 ③
由共需支付门票费为1290元可知,1≤a≤50,51≤b≤100,
得11a+13b=1290 ④,
解③④得:a=70人,b=40人
故两个部门的人数之差为70-40=30人,
故选:C.


科目:初中数学 来源: 题型:
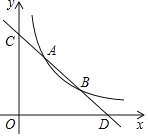
【题目】直线y1=kx+b与反比例函数![]() 的图象分别交于点A(m,4)和点B(n,2),与坐标轴分别交于点C和点D.
的图象分别交于点A(m,4)和点B(n,2),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)根据图象写出不等式kx+b﹣![]() ≤0的解集;
≤0的解集;
(3)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取n名学生作为样本,采用问卷调查的方式收集数据![]() 参与问卷调查的每名学生只能选择其中一项
参与问卷调查的每名学生只能选择其中一项![]() ,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
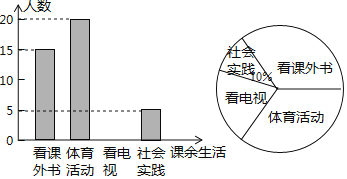
![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
![]() 若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
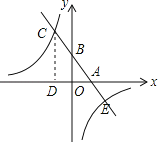
【题目】如图,已知一次函数y=kx+b(k,b为常数,k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=![]() (a≠0)的图象在第二象限交于点C,CD⊥x轴垂足为D点,若OB=2OA=3OD=6.
(a≠0)的图象在第二象限交于点C,CD⊥x轴垂足为D点,若OB=2OA=3OD=6.
(1)求反比例函数y=![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)直接写出关于x的不等式![]() >kx+b的解集.
>kx+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类别,每位同学仅选一项.根据调査结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | a | 0.5 |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | b | 1 |
根据图表提供的信息,回答下列问题:
(1)直接写出:a= .b= m= ;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请求选取的2人恰好是甲和乙的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在⊙O上,AB为直径,BD与过点C的切线垂直于D,BD与⊙O交于点E.
(1)求证:BC平分∠DBA;
(2)如果cos∠ABD=![]() ,OA=2,求DE的长.
,OA=2,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011广西崇左,18,3分)已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+b<m(am+b)(m≠1的实数);④(a+c)2<b2;⑤a>1.其中正确的项是( )

A. ①⑤ B. ①②⑤ C. ②⑤ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
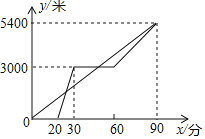
【题目】某景区的三个景点A,B,C在同一线路上.甲、乙两名游客从景点A出发,甲步行到景点C;乙先乘景区观光车到景点B,在B处停留一段时间后,再步行到景点C,甲、乙两人同时到达景点C.甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示:
(1)甲步行的速度为_____米/分,乙步行时的速度为_____米/分;
(2)求乙乘景区观光车时y与x之间的函数关系式;
(3)问甲出发多长时间与乙在途中相遇,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
(1)当轿车刚到乙地时,此时货车距离乙地 千米;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com