
【题目】如图,点C在⊙O上,AB为直径,BD与过点C的切线垂直于D,BD与⊙O交于点E.
(1)求证:BC平分∠DBA;
(2)如果cos∠ABD=![]() ,OA=2,求DE的长.
,OA=2,求DE的长.

【答案】(1)证明见解析;(2)1.
【解析】
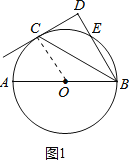
(1)如图1中,连接OC,由CD是⊙O的切线,推出OC⊥CD,由BD⊥CD,推出OC∥BD,推出∠OCB=∠CBD,由OC=OB,推出∠OCB=∠OBC,即可推出∠CBO=∠CBD;
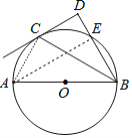
(2)如图2,连接AC、AE.易知四边形AEDC是直角梯形,求出CD、AE、BE长,则DE可求出.
(1)证明:如图1中,连接OC,
∵CD是⊙O的切线,
∴OC⊥CD,∵BD⊥CD,
∴OC∥BD,
∴∠OCB=∠CBD,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠CBO=∠CBD,
∴BC平分∠DBA;
(2)解:如图连接AC、AE.
∵cos∠ABD=![]() ,
,
∴∠ABD=60°,
由(1)可知,∠ABC=∠CBD=30°,
在Rt△ACB中,∵∠ACB=90°,∠ABC=30°,AB=4,
∴BC=ABcos30°=2![]() ,
,
在Rt△ABE中,∵∠AEB=90°,∠BAE=30°,AB=4,
∴BE=![]() AB=2,AE=2
AB=2,AE=2![]() ,
,
在Rt△CDB中,∵∠D=90°,∠CBD=30°,BC=2![]() ,
,
∴CD=![]() BC=
BC=![]() ,BD=3,
,BD=3,
∴DE=DB-BE=3-2=1.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】东坡商贸公司购进某种水果的成本为20元/kg,经过市场调研发现,这种水果在未来48天的销售单价p(元/kg)与时间t(天)之间的函数关系式为:
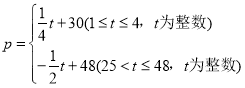 ,且其日销售量y(kg)与时间t(天)的关系如下表:
,且其日销售量y(kg)与时间t(天)的关系如下表:

(1)已知y与t之间的变化规律符合一次函数关系,试求在第30天的日销售量是多少?
(2)问哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘微将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形.后人借助这种分割方法所得的图形证明了勾股定理,如图所示若a=3,b=4,则该三角形的面积为( )
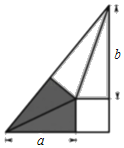
A. 10B. 12C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
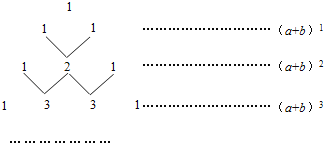
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左、右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等.
(1)(a+b)n展开式中项数共有 项.
(2)写出(a+b)5的展开式:(a+b)5= .
(3)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】团体购买某公园门票,票价如表,某单位现要组织其市场部和生产部的员工游览该公园.如果按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1290元;如果两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为990元.那么该公司这两个部门的人数之差为( )

A. 20B. 35C. 30D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的动点P和图形N,给出如下定义:如果Q为图形N上一个动点,P,Q两点间距离的最大值为dmax,P,Q两点间距离的最小值为dmin,我们把dmax+dmin的值叫点P和图形N间的“和距离”,记作d(P,图形N).
(1)如图1,正方形ABCD的中心为点O,A(3,3).
①点O到线段AB的“和距离”d(O,线段AB)=______;
②设该正方形与y轴交于点E和F,点P在线段EF上,d(P,正方形ABCD)=7,求点P的坐标.
(2)如图2,在(1)的条件下,过C,D两点作射线CD,连接AC,点M是射线CD上的一个动点,如果6![]() <d(M,线段AC)<6+3
<d(M,线段AC)<6+3![]() ,直接写出M点横坐标t取值范围.
,直接写出M点横坐标t取值范围.
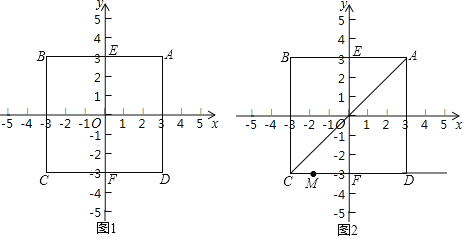
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同.小黑先从口袋里随机不放回地取出一个小球,记下数字为x;小白在剩下有三个小球中随机取出一个小球,记下数字y.
(1)计算由x、y确定的点(x,y)在函数![]() 图象上的概率;
图象上的概率;
(2)小黑、小白约定做一个游戏,其规则是:若x、y满足xy>6,则小黑胜;若x、y满足xy<6,则小白胜.这个游戏规则公平吗?说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
成绩x(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
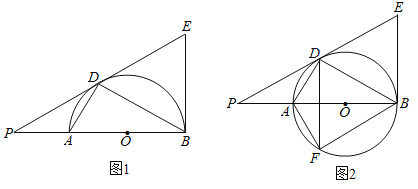
【题目】如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E
(1)证明:直线PD是⊙O的切线.
(2)如果∠BED=60°,![]() ,求PA的长.
,求PA的长.
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com