
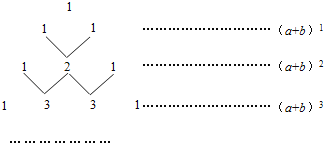
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左、右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等.
(1)(a+b)n展开式中项数共有 项.
(2)写出(a+b)5的展开式:(a+b)5= .
(3)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1.
【答案】(1)n+1;(2)a5+5a4b+10a3b2+10a2b3+5ab4+b5;(3)1.
【解析】
(1)根据规律,可知n+1项;
(2)根据规律,可知(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(3)根据规律得出原式=(2﹣1)5.
解:(1))(a+b)n展开式中项数共有n+1项,
故答案为n+1;
(2)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
故答案为a5+5a4b+10a3b2+10a2b3+5ab4+b5
(3)25﹣5×24+10×23﹣10×22+5×2﹣1
=25+5×24×(﹣1)+10×23×(﹣1)2+10×22×(﹣1)3+5×2×(﹣1)4+(﹣1)5
=(2﹣1)5
=1.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】绵阳中学为了进一步改善办学条件,决定计划拆除一部分旧校舍,建造新校舍.拆除旧校舍每平方米需80元,建造新校舍每平方米需要800元,计划在年内拆除旧校舍与建造新校舍共9 000平方米,在实施中为扩大绿化面积,新建校舍只完成了计划的90%而拆除旧校舍则超过了计划的10%,结果恰好完成了原计划的拆、建总面积.
(1)求原计划拆、建面积各是多少平方米?
(2)若绿化1平方米需要200元,那么把在实际的拆、建工程中节余的资金全部用来绿化,可绿化多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 三个顶点的坐标分别是
三个顶点的坐标分别是![]() .
.

(1)请在图中,画出![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 后得到的
后得到的![]() ,则
,则![]() 的正切值为 .
的正切值为 .
(2)以点![]() 为位似中心,将
为位似中心,将![]() 缩小为原来的
缩小为原来的![]() ,得到
,得到![]() ,请在图中
,请在图中![]() 轴左侧,画出
轴左侧,画出![]() ,若点
,若点![]() 是
是![]() 上的任意一点,则变换后的对应点
上的任意一点,则变换后的对应点![]() 的坐标是 .
的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
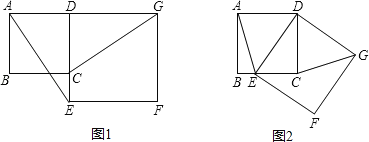
【题目】如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.
(1)试猜想AE与GC有怎样的关系(直接写出结论即可);
(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和CG.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.
(3)在(2)中,若E是BC的中点,且BC=2,则C,F两点间的距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:经过三角形一边中点,且平分三角形周长的直线叫做这个三角形在该边上的中分线,其中落在三角形内部的部分叫做中分线段.
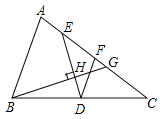
(1)如图,△ABC中,AC>AB,DE是△ABC在BC边上的中分线段,F为AC中点,过点B作DE的垂线交AC于点G,垂足为H,设AC=b,AB=c.
①求证:DF=EF;
②若b=6,c=4,求CG的长度;
(2)若题(1)中,S△BDH=S△EGH,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了为期一周的“敬老爱亲”社会活动,为了解情况,学生会随机调查了部分学生在这次活动中做家务的时间,并将统计的时间(单位:小时)分成5组,A:0.5≤x<1,B:1≤x<1.5,C:1.5≤x<2,D:2≤x<2.5,E:2.5≤x<3,制作成两幅不完整的统计图(如图).

请根据图中提供的信息,解答下列问题:
(1)学生会随机调查了 名学生;
(2)补全频数分布直方图;
(3)若全校有900名学生,估计该校在这次活动中做家务的时间不少于2.5小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
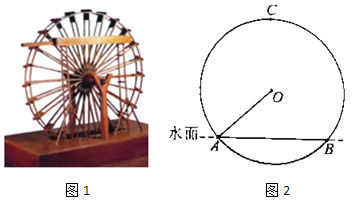
【题目】筒车是我国古代发明的一种水利灌溉工具.如图1,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理.如图2,筒车盛水桶的运行轨迹是以轴心O为圆心的圆.已知圆心在水面上方,且圆被水面截得的弦AB长为6米,∠OAB=41.3°,若点C为运行轨道的最高点(C,O的连线垂直于AB),求点C到弦AB所在直线的距离.(参考数据:sin41.3°≈0.66,cos41.3°≈0.75,tan41.3°≈0.88)
查看答案和解析>>
科目:初中数学 来源: 题型:
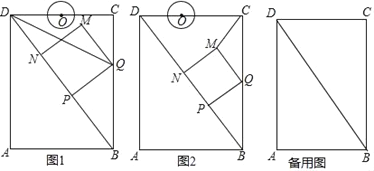
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上.点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,1cm半径作⊙O.点P与点D同时出发,设它们的运动时间为t(单位:s) (0≤t≤![]() ).
).
(1)如图1,连接DQ,若DQ平分∠BDC,则t的值为 s;
(2)如图2,连接CM,设△CMQ的面积为S,求S关于t的函数关系式;
(3)在运动过程中,当t为何值时,⊙O与MN第一次相切?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com