
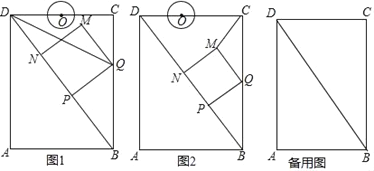
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上.点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,1cm半径作⊙O.点P与点D同时出发,设它们的运动时间为t(单位:s) (0≤t≤![]() ).
).
(1)如图1,连接DQ,若DQ平分∠BDC,则t的值为 s;
(2)如图2,连接CM,设△CMQ的面积为S,求S关于t的函数关系式;
(3)在运动过程中,当t为何值时,⊙O与MN第一次相切?
【答案】(1)1s; (2)S=﹣![]() t2+
t2+![]() t;(3)
t;(3)![]() .
.
【解析】试题分析:(1)由△DQC≌△DQP,推出DP=DC=6,在Rt△ADB中,BD=10,推出PB=4即可解决问题;
(2)过点M作MH⊥BC于点H,证明△HMQ∽△PQB,,由![]() =
=![]() ,得MH=
,得MH=![]() t,即可求得△CMQ的面积;
t,即可求得△CMQ的面积;
(3)设⊙O与MN相切于点E,连接OE,作OF⊥BD于点F,可证得△DFO∽△DCB,
由此![]() 即可解得:t值.
即可解得:t值.
试题解析:(1)∵四边形ABCD为矩形,
∴AB=CD=6cm、AD=BC=8cm,
则DB=10cm,
∵四边形PQMN为正方形,
∴∠BPQ=∠C=90°,
∵∠PBQ=∠CBD,
∴△BPQ∽△BCD,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
则BQ=5t、PQ=3t,
∴CQ=BC﹣BQ=8﹣5t,
∵DQ平分∠BDC,
∴QP=QC,即3t=8﹣5t,
解得:t=1,
故答案为:1;
(2)如图a,过点M作MH⊥BC于点H,
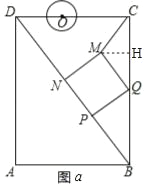
∴∠MHQ=∠QPB=∠MQP=90°,
则∠HMQ+∠HQM=∠PQB+∠HQM=90°,
∴∠HMQ=∠PQB,
∴△HMQ∽△PQB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
则MH=![]() t,
t,
∴S=![]() ×(8﹣5t)
×(8﹣5t)![]() t=﹣
t=﹣![]() t2+
t2+![]() t;
t;
(3)如图b,设⊙O与MN相切于点E,连接OE,作OF⊥BD于点F,
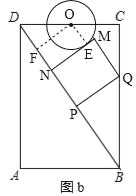
则四边形OENF为矩形,
∴OE=FN=1,∠DFO=∠C=90°,
∵∠FDO=∠CDB,
∴△DFO∽△DCB,
∴![]() ,即
,即![]() ,
,
解得:t=![]() .
.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 方程5x2=x有两个不相等的实数根
B. 方程x2﹣8=0有两个相等的实数根
C. 方程2x2﹣3x+2=0有两个整数根
D. 当k>![]() 时,方程(k﹣1)x2+2x﹣3=0有两个不相等的实数根
时,方程(k﹣1)x2+2x﹣3=0有两个不相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对平面直角坐标系中的点P(x,y),定义d=|x|+|y|,我们称d为P(x,y)的幸福指数.对于函数图象上任意一点P(x,y),若它的幸福指数d≥1恒成立,则称此函数为幸福函数,如二次函数y=x2+1就是一个幸福函数,理由如下:设P(x,y)为y=x2+1上任意一点,d=|x|+|y|=|x|+|x2+1|,∵|x|≥0,|x2+1|=x2+1≥1,∴d≥1.∴y=x2+1是一个幸福函数.
(1)若点P在反比例函数y=![]() 的图象上,且它的幸福指数d=2,请直接写出所有满足条件的P点坐标;
的图象上,且它的幸福指数d=2,请直接写出所有满足条件的P点坐标;
(2)一次函数y=﹣x+1是幸福函数吗?请判断并说明理由;
(3)若二次函数y=x2﹣(2m+1)x+m2+m(m>0)是幸福函数,试求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,
,![]() 平分
平分![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() 、
、![]() 分别是射线
分别是射线![]() 、
、![]() 上的动点(
上的动点(![]() 、
、![]() 不与点
不与点![]() 重合),连接
重合),连接![]() 交射线
交射线![]() 于点
于点![]() .设
.设![]() .
.

(1)如图1,若![]() ,则:①
,则:①![]() ______;②当
______;②当![]() 时,
时,![]() ______
______![]() .
.
(2)如图2,若![]() ,垂足为
,垂足为![]() ,则是否存在这样的
,则是否存在这样的![]() 的值,使得
的值,使得![]() 中存在两个相等的角?若存在,求出
中存在两个相等的角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AB=4.作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE.交射线BA于点F,连接AD、AE.当以A、D、M为顶点的三角形与△AEF全等时,DE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
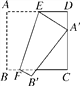
【题目】如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点B落在点B′处.已知折痕EF=13,则AE的长等于_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动——探究特殊的平行四边形.
问题情境
如图,在四边形ABCD中,AC为对角线,AB=AD,BC=DC.请你添加条件,使它们成为特殊的平行四边形.

提出问题
(1)第一小组添加的条件是“AB∥CD”,则四边形ABCD是菱形.请你证明;
(2)第二小组添加的条件是“∠B=90°,∠BCD=90°”,则四边形ABCD是正方形.请你证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:相等的实数看作同一个实数.有下列六种说法:
①数轴上有无数多个表示无理数的点;
②带根号的数不一定是无理数;
③每个有理数都可以用数轴上唯一的点来表示;
④数轴上每一个点都表示唯一一个实数;
⑤没有最大的负实数,但有最小的正实数;
⑥没有最大的正整数,但有最小的正整数.
其中说法错误的有_____(注:填写出所有错误说法的编号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店准备购进A、B两种型号的书包共50个进行销售,两种书包的进价、售价如下表所示:
书包型号 | 进价(元/个) | 售价(元/个) |
A型 | 200 | 300 |
B型 | 100 | 150 |
购进这50个书包的总费用不超过7300元,且购进B型书包的个数不大于A型书包个数的![]() .
.
(1)该文具店有哪几种进货方案?
(2)若该文具店购进的50个书包全部售完,则该文具店采用哪种进货方案,才能获得最大利润?最大利润是多少?(利润=售价﹣进价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com