
【题目】对平面直角坐标系中的点P(x,y),定义d=|x|+|y|,我们称d为P(x,y)的幸福指数.对于函数图象上任意一点P(x,y),若它的幸福指数d≥1恒成立,则称此函数为幸福函数,如二次函数y=x2+1就是一个幸福函数,理由如下:设P(x,y)为y=x2+1上任意一点,d=|x|+|y|=|x|+|x2+1|,∵|x|≥0,|x2+1|=x2+1≥1,∴d≥1.∴y=x2+1是一个幸福函数.
(1)若点P在反比例函数y=![]() 的图象上,且它的幸福指数d=2,请直接写出所有满足条件的P点坐标;
的图象上,且它的幸福指数d=2,请直接写出所有满足条件的P点坐标;
(2)一次函数y=﹣x+1是幸福函数吗?请判断并说明理由;
(3)若二次函数y=x2﹣(2m+1)x+m2+m(m>0)是幸福函数,试求出m的取值范围.
【答案】(1)满足条件的P点坐标为(﹣1,﹣1)或(1,1);
(2)一次函数y=﹣x+1是幸福函数,理由见解析;
(3)若二次函数y=x2﹣(2m+1)x+m2+m(m>0)是幸福函数,m的取值范围为m≥2.
【解析】试题分析:(1)设点P的坐标为(m, ![]() ),根据幸福指数的定义,即可得出关于m的分式方程,解之经检验即可得出结论;
),根据幸福指数的定义,即可得出关于m的分式方程,解之经检验即可得出结论;
(2)设P(x,y)为y=-x+1上的一点,分x<0、0≤x≤1和x>1三种情况找出d的取值范围,由此即可得出一次函数y=-x+1是幸福函数;
(3)设P(x,y)为y=x2-(2m+1)x+m2+m上的一点,由y=x2-(2m+1)x+m2+m=(x-m)(x-m-1)且m>0,可知分x≤0、0<x<m、m≤x≤m+1、x>m+1四段寻找m的取值范围,利用配方法以及二次函数的性质结合幸福函数的定义即可求出m的取值范围,综上即可得出结论.
试题解析:
解:(1)设点P的坐标为(m, ![]() ),
),
∴d=|m|+|![]() |=2,
|=2,
解得:m1=﹣1,m2=1,
经检验,m1=﹣1,m2=1是原分式方程的解,
∴满足条件的P点坐标为(﹣1,﹣1)或(1,1).
(2)一次函数y=﹣x+1是幸福函数,理由如下:
设P(x,y)为y=﹣x+1上的一点,d=|x|+|y|=|x|+|﹣x+1|,
当x<0时,d=|x|+|﹣x+1|=﹣x﹣x+1=1﹣2x>1;
当0≤x≤1时,d=|x|+|﹣x+1|=x﹣x+1=1;
当x>1时,d=|x|+|﹣x+1|=x+x﹣1=2x﹣1>1.
∴对于y=﹣x+1上任意一点P(x,y),它的幸福指数d≥1恒成立,
∴一次函数y=﹣x+1是幸福函数.
(3)设P(x,y)为y=x2-(2m+1)x+m2+m上的一点,d=|x|+|y|=|x|+|x2﹣(2m+1)x+m2+m|,
∵y=x2-(2m+1)x+m2+m=(x-m)(x-m-1),m>0,
∴分x≤0、0<x<m、m≤x≤m+1、x>m+1考虑.
①当x≤0时,d=|x|+|x2﹣(2m+1)x+m2+m|=﹣x+x2﹣(2m+1)x+m2+m=(x﹣m﹣1)2﹣m﹣1,
当x=0时,d取最小值,最小值为m2+m,
∴m2+m≥1,
解得:m≥![]() ;
;
②0<x<m时,d=|x|+|x2﹣(2m+1)x+m2+m|=x+x2﹣(2m+1)x+m2+m =(x﹣m)2+m﹣1≥1,
∵(x﹣m)2≥0,
∴m﹣1≥1,
解得:m≥2;
③当m≤x≤m+1时,d=|x|+|x2﹣(2m+1)x+m2+m|=x-x2+(2m+1)x-m2-m =﹣(x﹣m﹣1)2+m+1,
当x=m时,d取最小值,最小值为m,
∴m≥1;
④当x>m+1时,d=|x|+|x2﹣(2m+1)x+m2+m|=x+x2﹣(2m+1)x+m2+m=(x﹣m)2+m﹣1>m≥1,
∴m≥1.
综上所述:若二次函数y=x2-(2m+1)x+m2+m(m>0)是幸福函数,m的取值范围为m≥2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.
(1)求证:△AOE≌△COF;
(2)若∠EOD=30°,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上一点(不与端点
上一点(不与端点![]() 重合),
重合),![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() 交
交![]() 于点
于点![]() 、
、![]() .
.
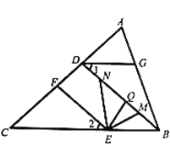
(1)请说明:![]() ;
;
(2)当点![]() 在
在![]() 上移动时,请写出
上移动时,请写出![]() 和
和![]() 之间满足的数量关系为______;
之间满足的数量关系为______;
(3)若![]() ,则当点
,则当点![]() 移动到使得
移动到使得![]() 时,请直接写出
时,请直接写出![]() ______(用含
______(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适宜采用全面调查方式(普查)的是( )
A. 对襄阳市中学生每天课外读书所用时间的调查
B. 对全国中学生心理健康现状的调查
C. 对七年级(2)班学生![]() 米跑步成绩的调查
米跑步成绩的调查
D. 对市面某品牌中性笔笔芯使用寿命的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
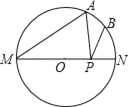
【题目】如图,MN是⊙O的直径,MN=2a,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则 PA+PB的最小值为_____.(用含a的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△DBC都是边长为2的等边三角形.

(1)以图1中的某个点为旋转中心,旋转△DBC,就能使△DBC与△ABC重合,则满足题意的点为: (写出符合条件的所有点);
(2)将△DBC沿BC方向平移得到△D1B1C1,如图2、图3,则四边形ABD1C1是平行四边形吗?证明你的结论;
(3)在(2)的条件下,当BB1= 时,四边形ABD1C1为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
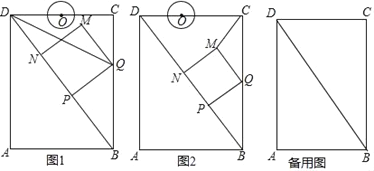
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上.点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,1cm半径作⊙O.点P与点D同时出发,设它们的运动时间为t(单位:s) (0≤t≤![]() ).
).
(1)如图1,连接DQ,若DQ平分∠BDC,则t的值为 s;
(2)如图2,连接CM,设△CMQ的面积为S,求S关于t的函数关系式;
(3)在运动过程中,当t为何值时,⊙O与MN第一次相切?
查看答案和解析>>
科目:初中数学 来源: 题型:
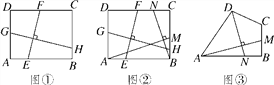
【题目】【探究证明】
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图①,在矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证: ![]() ;
;
【结论应用】
(2)如图②,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若![]() ,则
,则![]() 的值为 ;
的值为 ;
【联系拓展】
(3)如图③,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com