
【题目】如图1,△ABC和△DBC都是边长为2的等边三角形.

(1)以图1中的某个点为旋转中心,旋转△DBC,就能使△DBC与△ABC重合,则满足题意的点为: (写出符合条件的所有点);
(2)将△DBC沿BC方向平移得到△D1B1C1,如图2、图3,则四边形ABD1C1是平行四边形吗?证明你的结论;
(3)在(2)的条件下,当BB1= 时,四边形ABD1C1为矩形.
【答案】(1)B点、C点、BC的中点;(2)是平行四边形.理由见解析;(3)2
【解析】
(1)根据等边三角形的性质,得到四边形ABCD是菱形,从而再根据菱形是中心对称图形,得到旋转中心有B点、C点、BC的中点;
(2)根据平移的性质,得到BB1=CC1,根据等边三角形的性质,得到AC=B1D1,∠BB1D1=∠ACC1,从而得到△BB1D1≌△ACC1,则AB=C1D1,再根据两组对边分别平行的四边形是平行四边形即可证明;
(3)根据等边三角形的性质得出AD=BD=DD1,∠ADB=60°,进而得出∠BAD=90°,再利用矩形的判定得出即可.
解:(1)∵等边△ABC和等边△DBC有公共的底边BC,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形.
∴要旋转△DBC,使△DBC与△ABC重合,有三点分别为:B点、C点、BC的中点,
故答案为:B点、C点、BC的中点;
(2)四边形ABD1C1是平行四边形.理由如下:
根据平移的性质,得到BB1=CC1,
根据等边三角形的性质,得到AC=B1D1,∠BB1D1=∠ACC1,
∴△BB1D1≌△ACC1,
∴AC1=BD1,
又AB=C1D1,
∴四边形ABD1C1是平行四边形;
(3)当移动距离BB1=2时,四边形ABC1D1是矩形.
理由:连接BC1,AD1,
∵△ABD,△BDC都是边长为2的等边三角形,
∴AD=BD=DD1,∠ADB=60°,
∴∠DAD1=∠DD1A=30°,
∴∠BAD=60°+30°=90°,
∵由(2)可得出四边形ABC1D1是平行四边形,
∴平行四边形ABC1D1是矩形.
故答案为:2.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,为建设美丽农村,村委会打算在正方形地块甲和长方形地块乙上进行绿化.在两地块内分别建造一个边长为![]() 的大正方形花坛和四个边长为
的大正方形花坛和四个边长为![]() 的小正方形花坛(阴影部分),空白区域铺设草坪,记
的小正方形花坛(阴影部分),空白区域铺设草坪,记![]() 表示地块甲中空白处铺设草坪的面积,
表示地块甲中空白处铺设草坪的面积, ![]() 表示地块乙中空白处铺设草坪的面积.
表示地块乙中空白处铺设草坪的面积.

(1)![]() __ ,
__ ,![]() (用含
(用含![]() 的代数式表示并化简) .
的代数式表示并化简) .
(2)若![]() ,求
,求![]() 的值.
的值.
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形![]() 的顶点都在正方形网格的格点上,将三角形
的顶点都在正方形网格的格点上,将三角形![]() 经过平移后得到三角形
经过平移后得到三角形![]() ,其中点
,其中点![]() 是点
是点![]() 的对应点.
的对应点.

(1)画出平移后得到的三角形![]() ;
;
(2)连接![]() 、
、![]() ,则线段
,则线段![]() 、
、![]() 的关系为______;
的关系为______;
(3)四边形![]() 的面积为______(平方单位).
的面积为______(平方单位).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对平面直角坐标系中的点P(x,y),定义d=|x|+|y|,我们称d为P(x,y)的幸福指数.对于函数图象上任意一点P(x,y),若它的幸福指数d≥1恒成立,则称此函数为幸福函数,如二次函数y=x2+1就是一个幸福函数,理由如下:设P(x,y)为y=x2+1上任意一点,d=|x|+|y|=|x|+|x2+1|,∵|x|≥0,|x2+1|=x2+1≥1,∴d≥1.∴y=x2+1是一个幸福函数.
(1)若点P在反比例函数y=![]() 的图象上,且它的幸福指数d=2,请直接写出所有满足条件的P点坐标;
的图象上,且它的幸福指数d=2,请直接写出所有满足条件的P点坐标;
(2)一次函数y=﹣x+1是幸福函数吗?请判断并说明理由;
(3)若二次函数y=x2﹣(2m+1)x+m2+m(m>0)是幸福函数,试求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
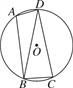
【题目】如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,
,![]() 平分
平分![]() ,点
,点![]() 在射线
在射线![]() 上,
上,![]() 、
、![]() 分别是射线
分别是射线![]() 、
、![]() 上的动点(
上的动点(![]() 、
、![]() 不与点
不与点![]() 重合),连接
重合),连接![]() 交射线
交射线![]() 于点
于点![]() .设
.设![]() .
.

(1)如图1,若![]() ,则:①
,则:①![]() ______;②当
______;②当![]() 时,
时,![]() ______
______![]() .
.
(2)如图2,若![]() ,垂足为
,垂足为![]() ,则是否存在这样的
,则是否存在这样的![]() 的值,使得
的值,使得![]() 中存在两个相等的角?若存在,求出
中存在两个相等的角?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AB=4.作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE.交射线BA于点F,连接AD、AE.当以A、D、M为顶点的三角形与△AEF全等时,DE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动——探究特殊的平行四边形.
问题情境
如图,在四边形ABCD中,AC为对角线,AB=AD,BC=DC.请你添加条件,使它们成为特殊的平行四边形.

提出问题
(1)第一小组添加的条件是“AB∥CD”,则四边形ABCD是菱形.请你证明;
(2)第二小组添加的条件是“∠B=90°,∠BCD=90°”,则四边形ABCD是正方形.请你证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;②3a+b<0;③﹣1≤a≤﹣![]() ;④4ac﹣b2>8a;
;④4ac﹣b2>8a;
其中正确的结论是( )

A.①③④ B.①②③ C.①②④ D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com