Question

【题目】如图，已知，，点是线段上一点（不与端点重合），、分别平分和交于点、.

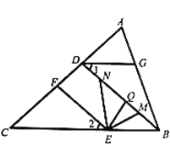
（1）请说明：；

（2）当点在上移动时，请写出和之间满足的数量关系为______；

（3）若，则当点移动到使得时，请直接写出______（用含的代数式表示）.

Answer 1

【答案】（1）见解析；（2）∠BQE=2∠BNE，证明见解析；（3）∠BEQ=，证明见解析.

【解析】

（1）根据，可证明,从而可证明∠1=∠DBC，根据可证明,从而证明BD//EF；

（2）通过角平分线和平行线的性质可证明∠BNE=∠NEQ，通过三角形的外角定理可证明∠BQE=2∠BNE；

（3）通过和三角形内角和定理可证明∠BEM=∠BNE，由（1）中∠BNE=∠NEQ可得∠BEM=∠NEQ，所以∠BEQ=∠MEN，通过角平分线的性质可得∠MEN==，即∠BEQ=.

（1）证明：

，

，

，

又，

，

∴BD//EF.

（2）∠BQE=2∠BNE，证明如下：

∵BD//EF

∴∠FEN=∠BNE

又∵EN平分∠QEF，

∴∠FEN=∠NEQ，

∴∠BNE=∠NEQ，

∵∠BNE+∠NEQ=∠BQE，

∴∠BQE=2∠BNE.

（3）∠BEQ=，证明如下：

∵EN平分∠QEF，

∴∠NEQ=，

同理可得∠QEM=，

∴∠MEN=，

∵，

∴∠2=，

∴∠BEF=180°-，

∴∠MEN=，

在△BEM中，∠CBD+∠BME+∠BEM=180°，

在△BEN中，∠CBD+∠BNE+∠BEN=180°，

∵，

∴∠BEM=∠BNE，

∵由（1）得∠BNE=∠NEQ，

∴∠BEM=∠NEQ，

∴∠BEQ=∠BEM+∠MEQ=∠NEQ+∠MEQ=.