
����Ŀ����ͼ1����֪������ABCD�ı�CD��������DEFG�ı�DE�ϣ�����AE��GC��
(1)�Բ���AE��GC�������Ĺ�ϵ(ֱ��д�����ۼ���)��
(2)��������DEFG�Ƶ�D��˳ʱ�뷽����ת��ʹ��E����BC���ϣ���ͼ2������AE��CG������Ϊ(1)�еĽ����Ƿ�����������������֤����������������˵�����ɣ�
(3)��(2)�У���E��BC���е㣬��BC��2����C��F�����ľ���Ϊ�� ����
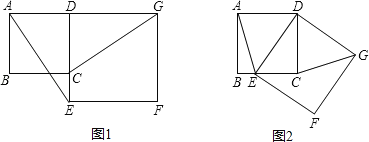
���𰸡�(1) AE��CG��AE��GC��(2)������֤���������� (3)![]() ��
��
��������
��1���۲�ͼ�Σ�AE��CG��λ�ù�ϵ�����Ǵ�ֱ����������֤���������ı���ABCD��DEFG���������Σ���֤����ADE�ա�CDG�����1����2�����ڡ�2����3���࣬���ԡ�1����3���࣬�ɴ˿ɵ�AE��GC��
��2���⣨1���Ľ�����Ȼ���������գ�1����Ľ��ⷽ������֤��ADE�ա�CDG���á�5����4�����ڡ�4����7���࣬����5����6���࣬��ô��6����7����ͼ֪��AEB����CEH��90������6������7+��CEH��90�����ɴ˵�֤��
��3����ͼ3�У���CM��DG��G��GN��CD��N��CH��FG��H�����ı���CMGH�Ǿ��Σ��ɵ�CM��GH��CH��GM����취���CH��HF�������ù��ɶ������ɽ�����⣮
(1)AE��CG��AE��GC��
֤�����ӳ�GC��AE�ڵ�H��
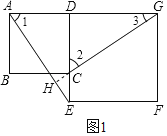
��������ABCD��������DEFG��
AD��DC����ADE����CDG��90����
DE��DG��
���ADE�ա�CDG(SAS)��
��AE��CG����1����2
�ߡ�2+��3��90����
���1+��3��90����
���AHG��180����(��1+��3)��180����90����90����
��AE��GC��
(2)�𣺳�����
֤�����ӳ�AE��GC�ཻ�ڵ�H��
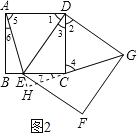
��������ABCD��������DEFG��
AD��DC��DE��DG����ADC����DCB����B����BAD����EDG��90����
���1����2��90������3��
���ADE�ա�CDG(SAS)��
��AE��CG����5����4��
�֡ߡ�5+��6��90������4+��7��180������DCE��180����90����90����
���6����7��
�֡ߡ�6+��AEB��90������AEB����CEH��
���CEH+��7��90����
���EHC��90����
��AE��GC��
(3)��ͼ3�У���CM��DG��G��GN��CD��N��CH��FG��H�����ı���CMGH�Ǿ��Σ��ɵ�CM��GH��CH��GM��
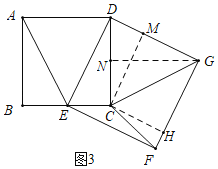
��BE��CE��1��AB��CD��2��
��AE��DE��CG�TDG��FG��![]() ��
��
��DE��DG����DCE����GND����EDC����DGN��
���DCE�ա�GND(AAS)��
��GCD��2��
��S��DCG��![]() CDNG��
CDNG��![]() DGCM��
DGCM��
��2��2��![]() CM��
CM��
��CM��GH��![]() ��
��
��MG��CH��![]() ��
��![]() ��
��
��FH��FG��FG��![]() ��
��
��CF��![]() ��
��![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ���ڵġ�MAN�����ڲ���һ��P�����P��ֱ��AM��AN�ľ���ֱ�Ϊd1��d2����![]() ��
��![]() ���������нϴ��һ��Ϊ��P����
���������нϴ��һ��Ϊ��P����![]() �ġ�ƫ�ʡ� . ��ƽ��ֱ������ϵxOy�У�
�ġ�ƫ�ʡ� . ��ƽ��ֱ������ϵxOy�У�
��1����M��N�ֱ�Ϊx�������ᣬy���������ϵ�������.
������P������Ϊ��1��5�������P����![]() �ġ�ƫ�ʡ�Ϊ____________��
�ġ�ƫ�ʡ�Ϊ____________��
������һ�����ڵ�Q��a��b������![]() �ġ�ƫ�ʡ�Ϊ1����a��b����Ĺ�ϵΪ____________��
�ġ�ƫ�ʡ�Ϊ1����a��b����Ĺ�ϵΪ____________��
��2����֪��A��4��0����B��2��![]() ��������OB��AB����C���߶�AB��һ���㣨��C�����A��B�غϣ�. ����C����
��������OB��AB����C���߶�AB��һ���㣨��C�����A��B�غϣ�. ����C����![]() �ġ�ƫ�ʡ�Ϊ2�����C�����ꣻ
�ġ�ƫ�ʡ�Ϊ2�����C�����ꣻ
��3����E��F�ֱ�Ϊx�������ᣬy���������ϵ������㣬����T������Ϊ��t��4����![]() ���Ե�TΪԲ�ģ��뾶Ϊ1��Բ. ��
���Ե�TΪԲ�ģ��뾶Ϊ1��Բ. ��![]() �ϵ����е㶼�ڵ�һ���ޣ��ҹ���
�ϵ����е㶼�ڵ�һ���ޣ��ҹ���![]() �ġ�ƫ�ʡ�������
�ġ�ƫ�ʡ�������![]() ��ֱ��д��t��ȡֵ��Χ.
��ֱ��д��t��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���γ��ھ���ij·�ڵĸ�Ӧ��B��C��ʱ�����۵Ƹ��ϵĵ��Ӿ������㵽������Ƭ������Ӧ��֮�����BCΪ6m���ڸ�Ӧ��B��C������õ��Ӿ���A�����Ƿֱ�Ϊ��ABD��18������ACD��14��������Ӿ��찲װ�����۵Ƹ��ϵĸ߶�AD�ij���
���ο����ݣ�sin14���0.242��cos14���0.97��tan14���0.25��sin18���0.309��cos18���0.951��tan18���0.325��
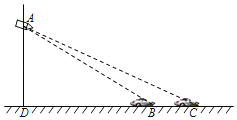
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������ĵĸ�����ǿ��������¸��
���壺�������ε��������������ȵĵ㣬�����������ε����ġ�
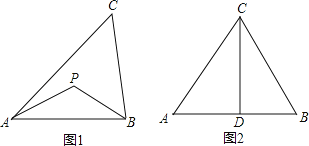
��������ͼ1����PA=PB�����PΪ��ABC�����ġ�
Ӧ�ã���ͼ2��CDΪ�ȱ�������ABC�ĸߣ�����P�ڸ�CD�ϣ���PD=![]() AB�����APB�Ķ�����
AB�����APB�Ķ�����
̽������֪��ABCΪֱ�������Σ�б��BC=5��AB=3������P��AC���ϣ���̽��PA�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ҹ��Ĵ�ͳ���գ�����ʳƷ��Ϊ�˽������ȥ�������ϺõĻ������ӡ�ˮ�����ӡ���ɳ���ӡ���������(�ֱ���A��B��C��D��ʾ)�����ֲ�ͬ��ζ�����ӵ�ϲ���������ij����������������˳������飬�����ݵ���������������������������ͳ��ͼ��
(1)���βμӳ�������ľ����ж����ˣ�
(2)������ͳ��ͼ����������
(3)С��ϲ���Ի������Ӻͺ������ӣ�����Ϊ�������������Ӹ�һ�������á��б�����������ͼ���ķ��������С��ͬʱѡ�л������Ӻͺ������ӵĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ������ֶ���λ������ǰ�У����С�������ǡ�����һ������ͼ����������εĹ��취�������ϵ�������1������ÿ������Ϊ���Ϸ���������֮�ͣ��������ˣ�a+b��n��nΪ����������չ��ʽ����a�Ĵ����ɴ�С��˳�����У���ϵ�����ɣ����磬���������е����е�������1��2��1��ǡ�ö�Ӧ��a+b��2��a2+2ab+b2չ��ʽ�е�ϵ���������е��ĸ���1��3��3��1��ǡ�ö�Ӧ�ţ�a+b��3��a3+3a2b+3ab2+b2չ��ʽ�е�ϵ���ȣ�
��1����a+b��nչ��ʽ������������ ���
��2��д����a+b��5��չ��ʽ����a+b��5���� ����
��3����������Ĺ��ɼ��㣺25��5��24+10��23��10��22+5��2��1��
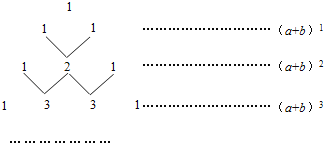
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ǰϦ��������ͨ婺ӹ�����������������500��ֱ�����������ϣ��ס������������е�·��y����λ���ף���ʱ��t����λ���֣�֮��ĺ�����ϵʽ��ͼ��ʾ������ͼ���ṩ����Ϣ��������˵�����ټӱ��Ҷ���ǰ0.5�ֵ����յ�ڵ�����1����ʱ���ӱ��Ҷ����50�ע۵�����![]() ����ʱ�������ҶӢܵ������Ҷ�ʱ�����ӻ��е�·�̶���300�����д�����ǣ�������
����ʱ�������ҶӢܵ������Ҷ�ʱ�����ӻ��е�·�̶���300�����д�����ǣ�������
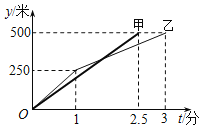
A. ��B. ��C. ��D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
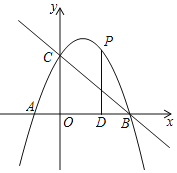
����Ŀ����ͼ��������![]() �������ύ��ֱ�Ϊ
�������ύ��ֱ�Ϊ![]() ��
��![]() ��
��![]() ����ֱ��BC��
����ֱ��BC��
![]() �������ߵĽ���ʽ��
�������ߵĽ���ʽ��
![]() ��PΪ�������ϵ�һ������һ���㣬����P��
��PΪ�������ϵ�һ������һ���㣬����P��![]() ���ڵ�D�����P�ĺ�����Ϊ
���ڵ�D�����P�ĺ�����Ϊ![]() ����
����![]() �����S��t�ĺ�����ϵʽ��
�����S��t�ĺ�����ϵʽ��
![]() ����ͬ
����ͬ![]() ����
����![]() ��
��![]() ���ƣ����P�����꣮
���ƣ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
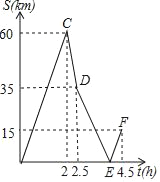
����Ŀ��A��B�������150km���ס��������Ⱥ��A�س�����B����ʻ������Ħ�г�������ʻ���ҿ�������;���ٶ�ֻ�ı�һ�Σ���ͼ��ʾ���Ǽס�������֮��ľ���S����ʱ��t�ĺ���ͼ��F��ʵ���������ҿ���������B�أ��������ͼ�����������⣺
��1��������ٶȣ�
��2�������ǰ�����ε��ٶȣ��������E�����ꣻ
��3�����ס����������10kmʱ����t��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com