
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于E,过点A作AF⊥AC于F交⊙O于D,连接DE,BE,BD
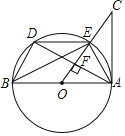
(1)求证:∠C=∠BED;
(2)若AB=12,tan∠BED=![]() ,求CF的长.
,求CF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据切线性质、垂直的性质、直角三角形的两个锐角互余的性质求得∠C+∠AOC=∠AOC+∠BAD=90°,即∠C=∠BAD;然后由圆周角定理推知∠BED=∠BAD;最后由等量代换得∠C=∠BED;
(2)根据锐角三角函数的定义求出AC,OC的长,求出AF长,则答案可求出.
(1)证明:∵AB是⊙O的直径,CA切⊙O于A,
∴∠C+∠AOC=90°;
又∵OC⊥AD,
∴∠OFA=90°,
∴∠AOC+∠BAD=90°,
∴∠C=∠BAD.
又∵∠BED=∠BAD,
∴∠C=∠BED.
(2)解:由(1)知∠C=∠BAD,tan∠BED=![]() ,
,
∴tan∠C=![]() ,
,
∴tan∠C=![]() ,且OA=
,且OA=![]() AB=6,
AB=6,
∴![]() ,解得AC=8,
,解得AC=8,
∴![]() ,
,
根据∠OFA=∠OAC=90°,
∴OCAF=OAAC,
∴![]() .
.
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】满足下列条件的△ABC不是直角三角形的是( )
A.∠A:∠B:∠C=2:3:5B.∠A:∠B:∠C=3:4:5
C.∠A﹣∠B=∠CD.BC=3,AC=4,AB=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 E,F,G,H 分别是任意四边形 ABCD 中 AD,BD,CA,BC 的中点. 若四边形 EFGH 是菱形,则四边形 ABCD 的边需满足的条件是( )
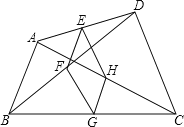
A. AB∥DC B. AC=BD C. AC⊥BD D. AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线![]() 与x轴、y轴分别交于点A,B,C是
与x轴、y轴分别交于点A,B,C是![]() 的中点,点D在直线
的中点,点D在直线![]() 上,以
上,以![]() 为直径的圆与直线
为直径的圆与直线![]() 的另一交点为E,交y轴于点F,G,已知
的另一交点为E,交y轴于点F,G,已知![]() ,
,![]() ,则
,则![]() 的长是______.
的长是______.
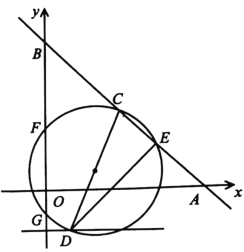
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 y=﹣x2+bx+c 与 x 轴交于 A、B 两点,与 y 轴交于点 C ,点 A 的坐标为(-1,0),点 C 的坐标为(0,3),点D和点 C 关于抛物线的对称轴对称,直线 AD 与 y 轴交于点 E .
(1)求抛物线的解析式;
(2)如图,直线 AD 上方的抛物线上有一点 F,过点 F 作 FG⊥AD 于点 G,作 FH 平行于 x 轴交直线 AD 于点 H,求△FGH 周长的最大值.
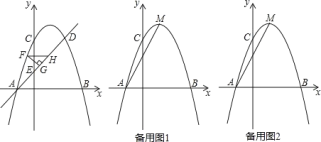
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加![]() kΩ.
kΩ.
(1)求R和t之间的关系式;
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.

查看答案和解析>>
科目:初中数学 来源: 题型:
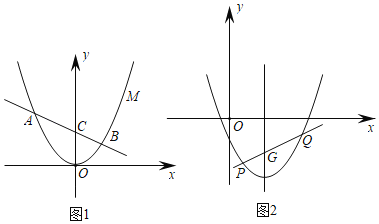
【题目】如图1,抛物线y=ax2过定点M(![]() ,
,![]() ),与直线AB:y=kx+1相交于A、B两点.
),与直线AB:y=kx+1相交于A、B两点.
(1)若k=﹣![]() ,求△ABO的面积.
,求△ABO的面积.
(2)若k=﹣![]() ,在抛物线上的点P,使得△ABP的面积是△ABO面积的两倍,求P点坐标.
,在抛物线上的点P,使得△ABP的面积是△ABO面积的两倍,求P点坐标.
(3)将抛物线向右平移两个单位,再向下平移两个单位,得到抛物线C2,如题图2,直线y=kx﹣2(k+![]() )与抛物线C2的对称轴交点为G,与抛物线C2的交点为P、Q两点(点P在点Q的左侧),试探究
)与抛物线C2的对称轴交点为G,与抛物线C2的交点为P、Q两点(点P在点Q的左侧),试探究![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com