
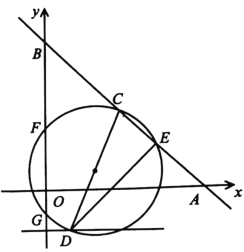
【题目】如图直线![]() 与x轴、y轴分别交于点A,B,C是
与x轴、y轴分别交于点A,B,C是![]() 的中点,点D在直线
的中点,点D在直线![]() 上,以
上,以![]() 为直径的圆与直线
为直径的圆与直线![]() 的另一交点为E,交y轴于点F,G,已知
的另一交点为E,交y轴于点F,G,已知![]() ,
,![]() ,则
,则![]() 的长是______.
的长是______.
【答案】![]()
【解析】
如图,设CD的中点为O′,设直线BA交直线y=﹣2于M,直线y=﹣2交y轴于P,作CH⊥OB于H,连接O′F,作AJ⊥DM于J,O′N⊥FG于N.首先利用等腰直角三角形的性质和条件![]() 可确定A,B,C的坐标,再设D(m,﹣2),进而可得O′N与O′F的长,而FN=
可确定A,B,C的坐标,再设D(m,﹣2),进而可得O′N与O′F的长,而FN=![]() ,然后在Rt△O′FN中利用勾股定理构建方程即可求出m,问题即得解决.
,然后在Rt△O′FN中利用勾股定理构建方程即可求出m,问题即得解决.
解:如图,设CD的中点为O′,设直线BA交直线y=﹣2于M,直线y=﹣2交y轴于P,作CH⊥OB于H,连接O′F,作AJ⊥DM于J,O′N⊥FG于N.
∵CD是⊙O′的直径,∴∠CED=90°,
∵直线y=﹣x+m(m>0)与x轴、y轴分别交于点A,B,
∴A(m,0),B(0,m),
∴OA=OB,∴∠OAB=45°,
∵OA∥DM,∴∠EMD=∠OAB=45°,
∵∠DEM=90°,∴ED=EM,
∴EC+ED=EC+EM=CM=![]() ,
,
∵JA⊥DM,∴∠AJM=90°,
∴AJ=JM=2,AM=2![]() ,
,
∴BC=CA=4![]() ,∴AB=8
,∴AB=8![]() ,∴BO=AO=8,
,∴BO=AO=8,
∴A(8,0),B(0,8),C(4,4),
设D(m,﹣2),则O′(![]() (m+4),1),
(m+4),1),
∴O′N=![]() (m+4),O′F=
(m+4),O′F=![]() CD=
CD=![]() ,
,
∵O′N⊥FG,∴FN=![]() ,
,
在Rt△O′FN中,由勾股定理,得:![]() ,解得m=1,
,解得m=1,
∴CD=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】为了解某市区九年级学生每天的健身活动情况,随机从市区九年级的12000名学生中抽取了500名学生,对这些学生每天的健身活动时间进行统计整理,作出了如下不完整的统计图(每组数据含最小值不含最大值,统计数据全部为整数),请根据以下信息解答如下问题:
时间/分 | 频数 | 频率 |
30~40 | 25 | 0.05 |
40~50 | 50 | 0.10 |
50~60 | 75 | b |
60~70 | a | 0.40 |
70~80 | 150 | 0.30 |
(1)a=_______,b=_______;
(2)请补全频数分布直方图;
(3)学生每天健身时间的中位数会落在哪个时间段?
(4)若每天健身时间在60分钟以上为符合每天“阳光一小时”的规定,则符合规定的学生人数大约是多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第 x 天的成本 y(元/件)与 x(天)之间的关系如图所示,并连续 60 天均以 80 元/件的价格出售, 第 x 天该产品的销售量 z(件)与 x(天)满足关系式 z=x+15.
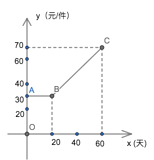
(1)第 25 天,该商家的成本是 元,获得的利润是 元;
(2)设第 x 天该商家出售该产品的利润为 w 元.
①求 w 与 x 之间的函数关系式;
②求出第几天的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°.
(1)如图①,点O在斜边AB上,以点O为圆心,OB长为半径的圆交AB于点D,交BC于点E,与边AC相切于点F.求证:∠1=∠2;
(2)在图②中作⊙M,使它满足以下条件:①圆心在边AB上;②经过点B;③与边AC相切.(尺规作图,只保留作图痕迹,不要求写出作法)
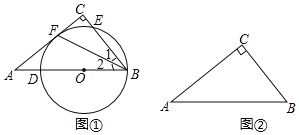
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于E,过点A作AF⊥AC于F交⊙O于D,连接DE,BE,BD
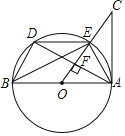
(1)求证:∠C=∠BED;
(2)若AB=12,tan∠BED=![]() ,求CF的长.
,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,以AB为直径作⊙O,交BC边于点D,交AC边于点F,作DE⊥AC于点E.
(1)求证:DE是⊙O的切线;
(2)若△ABC的边长为4,求EF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() x﹣4与抛物线y=
x﹣4与抛物线y=![]() +bx+c交于坐标轴上两点A、C,抛物线与x轴另一交点为点B;
+bx+c交于坐标轴上两点A、C,抛物线与x轴另一交点为点B;
(1)求抛物线解析式;
(2)若动点D在直线AC下方的抛物线上;
①作直线BD,交线段AC于点E,交y轴于点F,连接AD;求△ADE与△CEF面积差的最大值,及此时点D的坐标;
②如图2,作DM⊥直线AC,垂足为点M,是否存在点D,使△CDM中某个角恰好是∠ACO的一半?若存在,直接写出点D的横坐标;若不存在,说明理由.
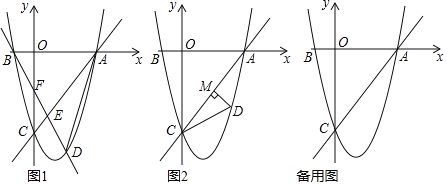
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,∠ACB=90°,AC=BC,E为外角∠BCD平分线上一动点(不与点C重合),点E关于直线BC的对称点为F,连接BE,连接AF并延长交直线BE于点G.
(1)求证:AF=BE;
(2)用等式表示线段FG,EG与CE的数量关系,并证明.
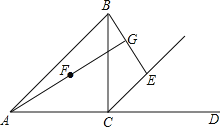
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com