
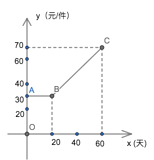
【题目】某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第 x 天的成本 y(元/件)与 x(天)之间的关系如图所示,并连续 60 天均以 80 元/件的价格出售, 第 x 天该产品的销售量 z(件)与 x(天)满足关系式 z=x+15.
(1)第 25 天,该商家的成本是 元,获得的利润是 元;
(2)设第 x 天该商家出售该产品的利润为 w 元.
①求 w 与 x 之间的函数关系式;
②求出第几天的利润最大,最大利润是多少?
【答案】(1)35,1800;(2)①![]() ;②第27或28天的利润最大,最大为1806元.
;②第27或28天的利润最大,最大为1806元.
【解析】
(1)根据已知条件可知第25天时的成本为35元,此时的销售量为40,则可求得第25天的利润.
(2)①利用每件利润×总销量=总利润,分当0<x≤20时与20<x≤60时,分别列出函数关系式;
②利用一次函数及二次函数的性质即可解答.
解:(1)由图象可知,此时的销售量为z=25+15=40(件),
设直线BC的关系为y=kx+b,将B(20,30)、C(60,70)代入
得:![]() ,解得:k=1,b=10,
,解得:k=1,b=10,
∴y=x+10,
∴第 25 天,该商家的成本是y=25+10=35(元)
则第25天的利润为:(8035)×40=1800(元);
故答案为:35,1800;
(2)①当0<x≤20时,![]() ;
;
当20<x≤60时,![]() ,
,
∴ ![]()
②当0<x≤20时,∵50>0,w随x的增大而增大,
∴当x=20时,w=50×20+750=1750(元),
当20<x≤60时,![]() ,
,
∵-1<0,抛物线开口向下,对称轴为![]() ,
,
当x=27与x=28时,![]() (元)
(元)
∵1806>1750,
∴第27或28天的利润最大,最大为1806元.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】“十三五”以来,山西省共解决372个村、35.8万农村人口的饮水型氟超标问题,让农村群众真正喝上干净水、放心水、安全水.某公司抓住商机,根据市场需求代理![]() ,
,![]() 两种型号的净水器,已知每台
两种型号的净水器,已知每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型,
型,![]() 型净水器的进价各是多少元?
型净水器的进价各是多少元?
(2)该公司计划购进![]() ,
,![]() 两种型号的净水器共55台进行试销,其中
两种型号的净水器共55台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买两种净水器的总资金不超过10.8万元.则最多可购进
台,购买两种净水器的总资金不超过10.8万元.则最多可购进![]() 型号净水器多少台?
型号净水器多少台?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
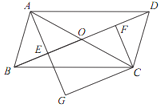
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF=![]() ;④S△AEF=
;④S△AEF=![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①相等的弦所对的圆心角相等;②对角线相等的四边形是矩形;③正六边形的中心角为60°;④对角线互相平分且相等的四边形是菱形;⑤计算![]() 的结果为7;⑥函数y=
的结果为7;⑥函数y=![]() 的自变量x的取值范围是x>﹣1;⑦
的自变量x的取值范围是x>﹣1;⑦![]() 的运算结果是无理数.其中正确的是____(填序号即可)
的运算结果是无理数.其中正确的是____(填序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
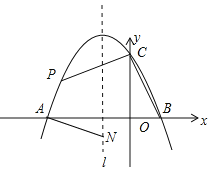
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其对称轴1为
,其对称轴1为![]() .
.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点![]() 在第二象限内的抛物线上,动点
在第二象限内的抛物线上,动点![]() 在对称轴1上.
在对称轴1上.
①当![]() ,且
,且![]() 时,求此时点
时,求此时点![]() 的坐标;
的坐标;
②当四边形![]() 的面积最大时,求四边形
的面积最大时,求四边形![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
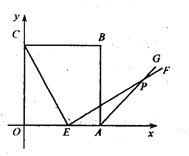
【题目】如图,边长为5的正方形 ![]() 的顶点
的顶点![]() 在坐标原点处,点
在坐标原点处,点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 是
是![]() 边上的点(不与点
边上的点(不与点![]() 重合)
重合)![]() ,且与正方形外角平分线
,且与正方形外角平分线![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)若点![]() 坐标为
坐标为![]() 时,①在
时,①在![]() 轴上是否存在点
轴上是否存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形?若存在,求出点
是平行四边形?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
②在平面内是否存在点![]() ,使四边形
,使四边形![]() 为正方形,若存在,请直接写出
为正方形,若存在,请直接写出![]() 点坐标,若不存在,说明理由.
点坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某中学学生的身高情况,随机对该校男、女生的身高进行抽样调查.抽取的样本中,男、女生的人数相同,根据所得数据绘制成如图所示的统计图表.

组别 | 男女生身高(cm) |
A | 150≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根据图表中提供的信息,回答下列问题:
(1)在样本中,男生身高的中位数落在__________组(填组别序号),女生身高在B组的有__________人;
(2)在样本中,身高在170≤x<175之间的共有__________人,人数最多的是__________组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在160≤x<170之间的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com