
【题目】“十三五”以来,山西省共解决372个村、35.8万农村人口的饮水型氟超标问题,让农村群众真正喝上干净水、放心水、安全水.某公司抓住商机,根据市场需求代理![]() ,
,![]() 两种型号的净水器,已知每台
两种型号的净水器,已知每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型,
型,![]() 型净水器的进价各是多少元?
型净水器的进价各是多少元?
(2)该公司计划购进![]() ,
,![]() 两种型号的净水器共55台进行试销,其中
两种型号的净水器共55台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买两种净水器的总资金不超过10.8万元.则最多可购进
台,购买两种净水器的总资金不超过10.8万元.则最多可购进![]() 型号净水器多少台?
型号净水器多少台?

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
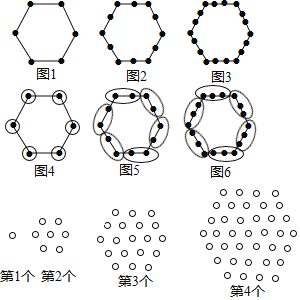
【题目】“分块计数法”:对有规律的图形进行计数时,有些题可以采用“分块计数”的方法.
例如:图1有6个点,图2有12个点,图3有18个点,……,按此规律,求图10、图n有多少个点?
我们将每个图形分成完全相同的6块,每块黑点的个数相同(如图),这样图1中黑点个数是6×1=6个;图2中黑点个数是6×2=12个:图3中黑点个数是6×3=18个;所以容易求出图10、图n中黑点的个数分别是 、 .
请你参考以上“分块计数法”,先将下面的点阵进行分块(画在答题卡上),再完成以下问题:
(1)第5个点阵中有 个圆圈;第n个点阵中有 个圆圈.
(2)小圆圈的个数会等于271吗?如果会,请求出是第几个点阵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
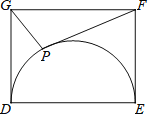
A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
![]() 若该抛物线经过点
若该抛物线经过点![]() ,试求
,试求![]() 的值及抛物线的顶点坐标.
的值及抛物线的顶点坐标.
![]() 求此抛物线的顶点坐标(用含
求此抛物线的顶点坐标(用含![]() 的代数式表示) ,并证明:不论
的代数式表示) ,并证明:不论![]() 为何值,该抛物线的顶点都在同一条直线
为何值,该抛物线的顶点都在同一条直线![]() 上.
上.
![]() 直线
直线![]() 截抛物线所得的线段长是否为定值?若是,请求出这个定值;若不是,请说明理由.
截抛物线所得的线段长是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
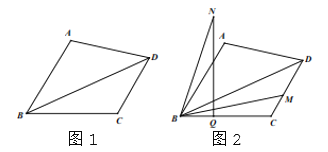
【题目】在四边形ABCD中,AB∥CD,∠ABC=60°,AB=BC=4,CD=3.
(1)如图1,求△BCD的面积;
(2)如图2,M是CD边上一点,将线段BM绕点B逆时针旋转60°,可得线段BN,过点N作NQ⊥BC,垂足为Q,设NQ=n,BQ=m,求n关于m的函数解析式.(自变量m的取值范围只需直接写出)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
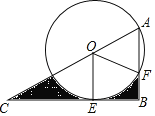
【题目】如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE、OF,则图中阴影部分的面积是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
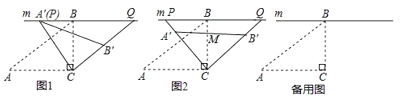
【题目】在![]() 中,
中,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() (点
(点![]() 的对应点分别为
的对应点分别为![]() ).
).
(1)问题发现如图1,若![]() 与
与![]() 重合时,则
重合时,则![]() 的度数为____________;
的度数为____________;
(2)类比探究:如图2,设![]() 与BC的交点为
与BC的交点为![]() ,当
,当![]() 为
为![]() 的中点时,求线段
的中点时,求线段![]() 的长;
的长;
(3)拓展延伸在旋转过程中,当点![]() 分别在
分别在![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值.若存在,直接写出四边形
的面积是否存在最小值.若存在,直接写出四边形![]() 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第 x 天的成本 y(元/件)与 x(天)之间的关系如图所示,并连续 60 天均以 80 元/件的价格出售, 第 x 天该产品的销售量 z(件)与 x(天)满足关系式 z=x+15.
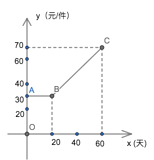
(1)第 25 天,该商家的成本是 元,获得的利润是 元;
(2)设第 x 天该商家出售该产品的利润为 w 元.
①求 w 与 x 之间的函数关系式;
②求出第几天的利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com