
【题目】在![]() 中,
中,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() (点
(点![]() 的对应点分别为
的对应点分别为![]() ).
).
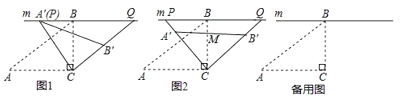
(1)问题发现如图1,若![]() 与
与![]() 重合时,则
重合时,则![]() 的度数为____________;
的度数为____________;
(2)类比探究:如图2,设![]() 与BC的交点为
与BC的交点为![]() ,当
,当![]() 为
为![]() 的中点时,求线段
的中点时,求线段![]() 的长;
的长;
(3)拓展延伸在旋转过程中,当点![]() 分别在
分别在![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值.若存在,直接写出四边形
的面积是否存在最小值.若存在,直接写出四边形![]() 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由.
【答案】(1)60![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由旋转可得:AC=A'C=2,进而得到BC=![]() ,依据∠A'BC=90°,可得
,依据∠A'BC=90°,可得![]() ,即可得到∠A'CB=30°,∠ACA'=60°;
,即可得到∠A'CB=30°,∠ACA'=60°;
(2)根据M为A'B'的中点,即可得出∠A=∠A'CM,进而得到![]() ,依据tan∠Q=tan∠A=
,依据tan∠Q=tan∠A=![]() ,即可得到BQ=BC×
,即可得到BQ=BC×![]() =2,进而得出PQ=PB+BQ=
=2,进而得出PQ=PB+BQ=![]() ;
;
(3)依据S四边形PA'B′Q=S△PCQ-S△A'CB'=S△PCQ-![]() ,即可得到S四边形PA'B′Q最小,即S△PCQ最小,而S△PCQ=
,即可得到S四边形PA'B′Q最小,即S△PCQ最小,而S△PCQ=![]() PQ×BC=
PQ×BC=![]() PQ,利用几何法或代数法即可得到S△PCQ的最小值=3,S四边形PA'B′Q=3-
PQ,利用几何法或代数法即可得到S△PCQ的最小值=3,S四边形PA'B′Q=3-![]() .
.
解:(1)由旋转可得:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(2)![]() 为
为![]() 的中点,
的中点,
![]() ,
,
山旋转可得,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(3)![]() 四边形
四边形![]()
![]() 四边形
四边形![]() 最小即
最小即![]() 最小,
最小,
![]() ,
,
取![]() 的中点
的中点![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,
当![]() 最小时,
最小时,![]() 最小,
最小,![]() ,即
,即![]() 与
与![]() 正合时,
正合时,![]() 最小,
最小,
![]() ,
,![]() ,
,
![]() 的最小值
的最小值![]() ,
,![]()
![]() 四边形
四边形![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
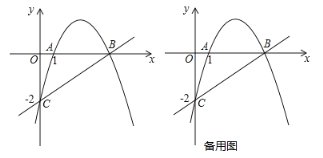
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,且点
,且点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,其对称轴为直线
,其对称轴为直线![]() .
.
(1)求这条抛物线的解析式;
(2)若在![]() 轴上方的抛物线上有点
轴上方的抛物线上有点![]() ,使
,使![]() 的内心恰好在
的内心恰好在![]() 轴上,求此时
轴上,求此时![]() 的面积;
的面积;
(3)在直线![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() ,过
,过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() 是否存在
是否存在![]() 点,使得以
点,使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出符合条件的点
相似?若存在,请求出符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十三五”以来,山西省共解决372个村、35.8万农村人口的饮水型氟超标问题,让农村群众真正喝上干净水、放心水、安全水.某公司抓住商机,根据市场需求代理![]() ,
,![]() 两种型号的净水器,已知每台
两种型号的净水器,已知每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型,
型,![]() 型净水器的进价各是多少元?
型净水器的进价各是多少元?
(2)该公司计划购进![]() ,
,![]() 两种型号的净水器共55台进行试销,其中
两种型号的净水器共55台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买两种净水器的总资金不超过10.8万元.则最多可购进
台,购买两种净水器的总资金不超过10.8万元.则最多可购进![]() 型号净水器多少台?
型号净水器多少台?

查看答案和解析>>
科目:初中数学 来源: 题型:
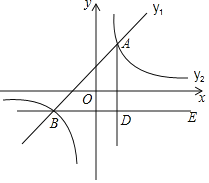
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 请直接写出
请直接写出![]() 时,x的取值范围;
时,x的取值范围;
![]() 过点B作
过点B作![]() 轴,
轴,![]() 于点D,点C是直线BE上一点,若
于点D,点C是直线BE上一点,若![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.
学生借阅图书的次数:
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次以上 |
人数 | 7 | 13 |
| 10 | 3 |

请你根据统计图表中的信息,解答下列问题:
(1)![]() ____________,
____________,![]() ____________;
____________;
(2)该调查统计数据的中位数是___________次;
(3)扇形统计图中,“3次”所对应扇形的圆心角的度数是____________;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日,全省各地市的2019年初中毕业升学体育考试工作正依照某省教育厅的具体要求在有条不紊的进行当中,某中学在正式考试前,为了让同学们在中招体育考试中获得理想成绩,同时为了了解学生的当前水平,按批次进行了模拟考试,并随机抽取若干名学生问卷调查,现将调查结果绘制成如下不完整的统计图表:
组别 | 成绩范围x(分) | 频数(人数) |
A | 60<x≤70 | 54 |
B | 50<x≤60 | m |
C | 40<x≤50 | n |
D | 30<x≤40 | 6 |
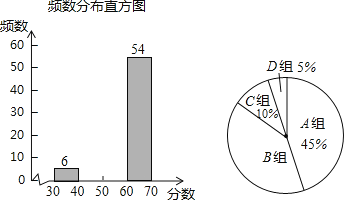
(1)这次调查的总人数有 人,表中的m= ,n= ;
(2)扇形统计图中B组对应的圆心角为 °;
(3)请补全频数分布直方图;
(4)若该校九年级共有学生2700名,且都参加了正式的初中毕业升学体育考试,小华也参加了这次考试并得了67分,若规定60分以上为优秀,体育老师想要在获得优秀的学生中随机抽出1名,作为学生代表向学弟学妹们传授经验,求抽到小华的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
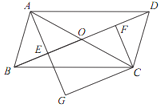
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
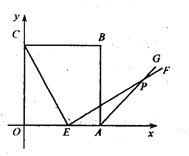
【题目】如图,边长为5的正方形 ![]() 的顶点
的顶点![]() 在坐标原点处,点
在坐标原点处,点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 是
是![]() 边上的点(不与点
边上的点(不与点![]() 重合)
重合)![]() ,且与正方形外角平分线
,且与正方形外角平分线![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)若点![]() 坐标为
坐标为![]() 时,①在
时,①在![]() 轴上是否存在点
轴上是否存在点![]() ,使得四边形
,使得四边形![]() 是平行四边形?若存在,求出点
是平行四边形?若存在,求出点![]() 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
②在平面内是否存在点![]() ,使四边形
,使四边形![]() 为正方形,若存在,请直接写出
为正方形,若存在,请直接写出![]() 点坐标,若不存在,说明理由.
点坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com