
【题目】为了了解某中学学生的身高情况,随机对该校男、女生的身高进行抽样调查.抽取的样本中,男、女生的人数相同,根据所得数据绘制成如图所示的统计图表.

组别 | 男女生身高(cm) |
A | 150≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根据图表中提供的信息,回答下列问题:
(1)在样本中,男生身高的中位数落在__________组(填组别序号),女生身高在B组的有__________人;
(2)在样本中,身高在170≤x<175之间的共有__________人,人数最多的是__________组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在160≤x<170之间的学生有多少人?
【答案】(1)D;12;(2)10;C;(3)估计身高在160≤x<170之间的学生约有541人.
【解析】
(1)根据中位数的定义进行求解可得男生身高的中位数,由于抽取的男、女生人数相同,因此用40×(1–20%–35%–10%–5%)即可求得女生身高在B组的人数;
(2)将身高在170≤x<175之间的男、女生人数相加即可,分别求出A、B、C、D、E组的男、女生人数之和,比较即可确定;
(3)分别用男、女生人数乘以身高在160≤x<170之间的学生所占比例,然后相加即可得.
(1)∵在样本中,男生共有2+4+8+12+14=40(人),
∴中位数是第20和第21人的平均数,
∴男生身高的中位数落在D组,
女生身高在B组的人数有40×(1–20%–35%–10%–5%)=12(人),
故答案为:D;12;
(2)在样本中,身高在170≤x<175之间的人数共有8+40×5%=10(人),
∵A组人数为2+40×20%=10(人),
B组人数为4+12=32(人),
C组人数为12+40×35%=26人,
D组人数为14+40×10%=18(人),
E组人数为8+40×5%=10(人),
∴C组人数最多,
故答案为:10;C;
(3)500×![]() +480×(35%+10%)=541(人),
+480×(35%+10%)=541(人),
故估计身高在160≤x<170之间的学生约有541人.


科目:初中数学 来源: 题型:
【题目】某商家在购进一款产品时,由于运输成本及产品成本的提高,该产品第 x 天的成本 y(元/件)与 x(天)之间的关系如图所示,并连续 60 天均以 80 元/件的价格出售, 第 x 天该产品的销售量 z(件)与 x(天)满足关系式 z=x+15.
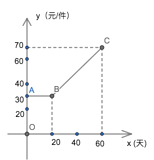
(1)第 25 天,该商家的成本是 元,获得的利润是 元;
(2)设第 x 天该商家出售该产品的利润为 w 元.
①求 w 与 x 之间的函数关系式;
②求出第几天的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地如图,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数图象;折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数图象;请根据图象解答下到问题:
(1)货车离甲地距离y(干米)与时间x(小时)之间的函数式为 ;
(2)当轿车与货车相遇时,求此时x的值;
(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个两位数,用![]() 表示十位上的数,用
表示十位上的数,用![]() 表示个位上的数.
表示个位上的数.
(1)用含![]() ,
,![]() 的式子表示这个两位数;
的式子表示这个两位数;
(2)把这个两位数个位上的数字与十位上的数字交换位置,得到一个新的两位数.
①若原数个位上的数是十位上的数的3倍,且新数与原数的差是36,求原来的两位数是多少?
②列式表示所得新数的平方与原数的平方的差(结果要化简),并判断其是11的倍数吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
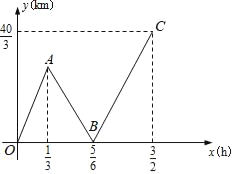
【题目】甲骑电动车、乙骑摩托车都从M地出发,沿一条笔直的公路匀速前往N地,甲先出发一段时间后乙再出发.甲,乙两人到达N地后均停止骑行,已知M,N两地相距![]() km,设甲行驶的时间为x(h),甲、乙两人之同的距离为y(km),表示y与x函数关系的图象如图所示.请你解决以下问题:
km,设甲行驶的时间为x(h),甲、乙两人之同的距离为y(km),表示y与x函数关系的图象如图所示.请你解决以下问题:
(1)求线段BC所在直线的函数表达式;
(2)分别求甲,乙的速度;
(3)填空:点A的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E,D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)求点C和点D的坐标;
(3)若点P在第一象限内的抛物线上,且S△ABP=4S△COE,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() 三点,已知
三点,已知![]()

![]() 求此抛物线的关系式;
求此抛物线的关系式;
![]() 设点
设点![]() 是线段
是线段![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 轴的平行线,交线段
轴的平行线,交线段![]() 于点
于点![]() 当
当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 点
点![]() 是抛物线上的一动点,当
是抛物线上的一动点,当![]() 中
中![]() 的面积最大时,请直接写出使
的面积最大时,请直接写出使![]() 的点
的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电器专营店的经营利润受地理位置、顾客消费能力等因素的影响,某品牌电脑专营店设有甲、乙两家分店,均销售A、B、C、D四种款式的电脑,每种款式电脑的利润如表1所示.现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式,统计各种款式电脑的销售数量,如表2所示.
表1:四种款式电脑的利润
电脑款式 | A | B | C | D |
利润(元/台) | 160 | 200 | 240 | 320 |
表2:甲、乙两店电脑销售情况
电脑款式 | A | B | C | D |
甲店销售数量(台) | 20 | 15 | 10 | 5 |
乙店销售数量(台)8 | 8 | 10 | 14 | 18 |
试运用统计与概率知识,解决下列问题:
(1)从甲店每月售出的电脑中随机抽取一台,其利润不少于240元的概率为 ;
(2)经市场调查发现,甲、乙两店每月电脑的总销量相当.现由于资金限制,需对其中一家分店作出暂停营业的决定,若从每台电脑的平均利润的角度考虑,你认为应对哪家分店作出暂停营业的决定?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生的课外阅读情况,七(1)班针对“你最喜爱的课外阅读书目”进行调查(每名学生必须选一类且只能选一类阅读书目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选类别人数统计表
类别 | 男生(人) | 女生(人) |
文学类 | 12 | 8 |
史学类 |
| 5 |
科学类 | 6 | 5 |
哲学类 | 2 |
|

根据以上信息解决下列问题
(1)![]() ,
,![]() ;
;
(2)扇形统计图中“科学类”所对应扇形圆心角度数为 ![]() ;
;
(3)从选哲学类的学生中,随机选取两名学生参加学校团委组织的辩论赛,请用树状图或列表法求出所选取的两名学生都是男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com