
【题目】如图,某沿海开放城市![]() 接到台风警报,在该市正南方向
接到台风警报,在该市正南方向![]() 的
的![]() 处有一台风中心,沿
处有一台风中心,沿![]() 方向以
方向以![]() 的速度向
的速度向![]() 移动,已知城市
移动,已知城市![]() 到
到![]() 的距离
的距离![]() .
.
(1)求台风中心经过多长时间从![]() 点移到
点移到![]() 点?
点?
(2)如果在距台风中心![]() 的圆形区域内都将有受到台风的破坏的危险,
的圆形区域内都将有受到台风的破坏的危险,
正在![]() 点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?
点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?
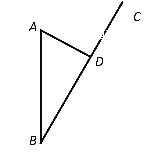
【答案】(1)4小时 (2)2.5
【解析】试题分析:首先根据勾股定理计算BD的长,再根据时间=路程÷速度进行计算;再根据在30千米范围内都要受到影响,先求出从点B到受影响的距离与结束影响的距离,再根据时间=路程÷速度计算,然后求出时间段即可.
试题解析:
(1)∵AB=100km,AD=60km,
∴在Rt△ABD中,根据勾股定理得
BD=![]() =80km,
=80km,
∴台风中心经过80÷20=4小时从B移动到D点;
(2)如图,∵距台风中心30km的圆形区域内都会受到不同程度的影响,
∴人们要在台风中心到达E点之前撤离,
∵BE=BD-DE=80-30=50km,
∴游人在50÷20=2.5小时内撤离才可脱离危险.



 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】今年参观“5.18”海交会的总人数约为489000人,将489000用科学记数法表示为( )
A.48.9×104
B.4.89×105
C.4.89×104
D.0.489×106
查看答案和解析>>
科目:初中数学 来源: 题型:
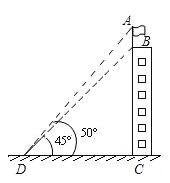
【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
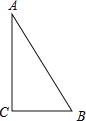
【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的面积;
(2)当t为几秒时,BP平分∠ABC;
(3)问t为何值时,△BCP为等腰三角形?
(4)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
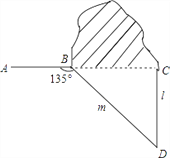
【题目】如图,修公路遇到一座山,于是要修一条隧道.为了加快施工进度,想在小山的另一侧同时施工.为了使山的另一侧的开挖点C在AB的延长线上,设想过C点作直线AB的垂线L,过点B作一直线(在山的旁边经过),与L相交于D点,经测量∠ABD=135°,BD=800米,求直线L上距离D点多远的C处开挖?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
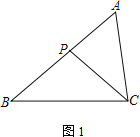
【题目】在△ABC中,P为边AB上一点.
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
(2) 若M为CP的中点,AC=2,
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
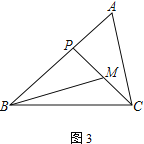
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com