
【题目】顺次连结对角线相等的四边形的四边中点所得图形是( )
A.正方形
B.矩形
C.菱形
D.以上都不对
【答案】C
【解析】如图:已知四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,AC=BD,
连接AC、BD,
∵E、F、G、H分别是边AB、BC、CD、DA的中点,
∴EF=![]() AC,GH=
AC,GH=![]() AC,GF=
AC,GF=![]() BD,EH=
BD,EH=![]() BD,
BD,
又∵AC=BD,
∴EF=GH=GF=EH,
∴四边形EFGH是菱形.
所以答案是:C.
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对菱形的判定方法的理解,了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号![]() 表示不大于
表示不大于![]() 的最大整数,称
的最大整数,称![]() 为a的根整数,例如:
为a的根整数,例如:![]() ,
,![]() =3.
=3.
(1)仿照以上方法计算:![]() =______;
=______;![]() =_____.
=_____.
(2)若![]() ,写出满足题意的x的整数值______.
,写出满足题意的x的整数值______.
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次![]()
![]()
![]() =1,这时候结果为1.
=1,这时候结果为1.
(3)对100连续求根整数,____次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx﹣2的图象经过点A、C,并与y轴交于点E,反比例函数y= ![]() 的图象经过点A.
的图象经过点A.
(1)点E的坐标是;
(2)求反比例函数的解析式;
(3)求当一次函数的值小于反比例函数的值时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,则有a2+b2=c2;如图(2),△ABC为锐角三角形时,小明猜想a2+b2>c2,理由如下:
设CD=x,在Rt△ADC中,AD2=b2-x2,
在Rt△ADB中,AD2=c2-(a-x)2,
则b2-x2=c2-(a-x)2,所以a2+b2=c2+2ax,
因为a>0,x>0,所以2ax>0,所以a2+b2>c2,
所以当△ABC为锐角三角形时a2+b2>c2.
所以小明的猜想是正确的.
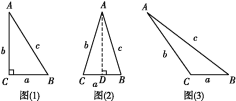
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系;
(2)证明你猜想的结论是否正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上两点A、B所表示的数分别为-3、1.
(1)写出线段AB的中点M所对应的数;
(2)若点P从B出发,以每秒2个单位长度的速度向左运动,运动时间为![]() 秒:
秒:
①用含![]() 的代数式表示点P所对应的数;
的代数式表示点P所对应的数;
②当BP=2AP时,求![]() 值。
值。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 y=![]() ,在下列结论中,错误的是( )
,在下列结论中,错误的是( )
A.图象位于第一、三象限
B.图象必经过点(﹣2,﹣3)
C.y随x的增大而增小
D.若x>2,则0<y<3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某儿童游乐园门票价格规定如下表:
购票张数 | 1~50张 | 51~100张 | 100张以上 |
每张票的价格 | 13元 | 11元 | 9元 |
某校七年级(1)、(2)两个班共102人今年6.1儿童节去游该游乐园,其中(1)班人数较少,不足50人。经估算,如果两个班都以班为单位购票,则一共应付1218元。问:
(1)两个班各有多少学生?
(2)如果两班联合起来,作为一个团体购票,可以节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图计算:
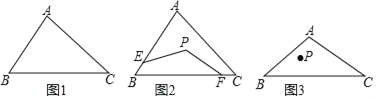
(1)已知△ABC,请用尺规在图1中△ABC内确定一个点P,使得点P到AB和BC的距离相等,且满足P到点B和点C的距离相等(不写作法,保留作图痕迹).
(2)如图2,如果点P是(1)中求作的点,点E、F分别在边AB、BC上,且PE=PF.
①若∠ABC=60°,求∠EPF的度数;
②若BE=2,BF=8,EP=5,求BP的长.
(3)如图3,如果点P是△ABC内一点,且点P到点B的距离是7,若∠ABC=45°,请分别在AB、BC上求作两个点M、N,使得△PMN的周长最小(不写作法,保留作图痕迹),则△PMN的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC 中,AB=AC,∠BAC=90°,D 是BC 上一点,EC⊥BC,EC=BD,DF=FE.

求证:(1)△ABD≌△ACE;
(2)AF⊥DE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com