
【题目】如图(1),在△ABC中,BC=a,AC=b,AB=c,若∠C=90°,则有a2+b2=c2;如图(2),△ABC为锐角三角形时,小明猜想a2+b2>c2,理由如下:
设CD=x,在Rt△ADC中,AD2=b2-x2,
在Rt△ADB中,AD2=c2-(a-x)2,
则b2-x2=c2-(a-x)2,所以a2+b2=c2+2ax,
因为a>0,x>0,所以2ax>0,所以a2+b2>c2,
所以当△ABC为锐角三角形时a2+b2>c2.
所以小明的猜想是正确的.
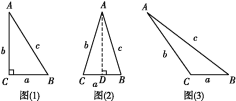
(1)请你猜想,当△ABC为钝角三角形时,a2+b2与c2的大小关系;
(2)证明你猜想的结论是否正确.
【答案】(1)a2+b2<c2;(2)证明见解析.
【解析】
(1)根据题意可猜测:当△ABC为钝角三角形时,a2+b2与c2的大小关系为:a2+b2<c2;
(2)过点A作AD⊥BC于点D;然后设CD=x,分别在Rt△ADC与Rt△ADB中,表示出AD2,即可证得结论.
(1)当△ABC为钝角三角形时,a2+b2与c2的大小关系为:a2+b2<c2;
(2)如图3,过点A作AD⊥BC于点D,设CD=x.
在Rt△ADC中,AD2=b2﹣x2.在Rt△ADB中,AD2=c2﹣(a+x)2,∴b2﹣x2=c2﹣(a+x)2,∴a2+b2=c2﹣2ax.
∵a>0,x>0,∴2ax>0,∴a2+b2<c2,∴当△ABC为钝角三角形时,a2+b2<c2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知点O(0,0),B(2,3),点A在坐标轴上,且S△AOB=6.
(1)求满足条件的点A的坐标;
(2)点C(﹣3,1),过O点直线l把三角形BOC分成面积相等的两部分,交BC于D,则D的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=90°,AB∥ED ,交BC于E,交 AC于F, DE = BC,![]() .
.

(1) 求证:△FCD 是等腰三角形
(2) 若AB=3.5cm,求CD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某地方政府决定在相距50km的A、B两站之间的公路旁E点,修建一个土特产加工基地,且使C、D两村到E点的距离相等,已知DA⊥AB于A,CB⊥AB于B,DA=30km,CB=20km,那么基地E应建在离A站多少千米的地方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,已知∠BAD=120°,∠EGF=60°,∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC,CD于点E,F.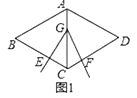
(1)如图2,当顶点G运动到与点A重合时,求证:EC+CF=BC;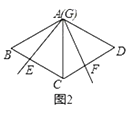
(2)知识探究:①如图3,当顶点G运动到AC中点时,探究线段EC,CF与BC的数量关系;
②在顶点G的运动过程中,若 ![]() =t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);
=t,请直接写出线段EC,CF与BC的数量关系(不需要写出证明过程);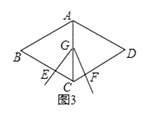
(3)问题解决:如图4,已知菱形边长为8,BG=7,CF= ![]() ,当t>2时,求EC的长度.
,当t>2时,求EC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班抽取6名同学参加体能测试,成绩如下:85,95,85,80,80,85.下列表述错误是( )
A.众数是85
B.平均数是85
C.方差是20
D.极差是15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( ).
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( ).
①作出AD的依据是SAS;②∠ADC=60°
③点D在AB的中垂线上;④S△DAC:S△ABD=1:2.

A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com