
分析 首先根据当x=2时,px7+qx5-6=2014,求出x=2时,px7+qx5的值是多少;然后分别求出x=-2时,px7+qx5、px5+qx3的值各是多少,即可求出px7+qx5-6,px5+qx3-6的值各是多少.
解答 解:∵当x=2时,px7+qx5-6=2014,
∴27p+25q-6=2014,
∴128p+32q=2020,
(1)当x=-2时,
px7+qx5-6=(-2)7p+(-2)5q-6
=-(128p+32q)-6
=-2020-6
=-2026
(2)当x=-2时,
px5+qx3-6=(-2)5p+(-2)3q-6
=-(32p+8q)-6
=-2020÷4-6
=-505-6
=-511
故答案为:-2026、-511.
点评 此题主要考查了代数式求值问题,要熟练掌握,解答此题的关键是求出x=-2时,px7+qx5、px5+qx3的值各是多少.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
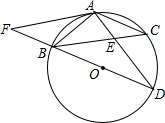 如图,在⊙O中,弦AB=AC,BD为⊙O的直径,AD交BC于E,AF∥BC交DB的延长线于点F,AE=2,ED=4.
如图,在⊙O中,弦AB=AC,BD为⊙O的直径,AD交BC于E,AF∥BC交DB的延长线于点F,AE=2,ED=4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com