阅读快车系列答案科目：初中数学 来源： 题型：
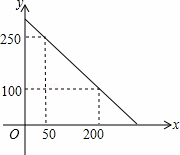
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒，乙品牌的进货单价是甲品牌进货单价的2倍，考虑各种因素，预计购进乙品牌文具盒的数量y（个）与甲品牌文具盒的数量x（个）之间的函数关系如图所示．当购进的甲、乙品牌的文具盒中，甲有120个时，购进甲、乙品牌文具盒共需7200元．
（1）根据图象，求y与x之间的函数关系式；
（2）求甲、乙两种品牌的文具盒进货单价；
（3）若该超市每销售1个甲种品牌的文具盒可获利4元，每销售1个乙种品牌的文具盒可获利9元，根据学生需求，超市老板决定，准备用不超过6300元购进甲、乙两种品牌的文具盒，且这两种品牌的文具盒全部售出后获利不低于1795元，问该超市有几种进货方案？哪种方案能使获利最大？最大获利为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
已知：如图，是由一个等边△ABE和一个矩形BCDE拼成的一个图形，
其中
B，C，D点的坐标分别为(1，2)，
(1，1)，(3，1)．
(1)求E点和A点的坐标；
(2)试以点P(0，2)为位似中
心，作出相似比为3的位
似图形A1B1C1D1E1，并写出
各对应点的坐标；
查看答案和解析>>
科目：初中数学 来源： 题型：
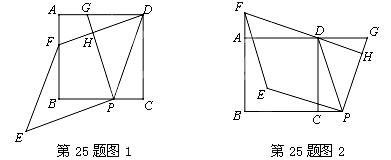
已知，四边形ABCD是正方形，点P在直线BC上，点G在直线AD上（P、G
不与正方形顶点重合，且在CD的同侧），PD=PG，DF⊥PG于点H，交直线AB于点F，
将线段PG绕点P逆时针旋转90°得到线段PE，连结EF.
(1)如图1，当点P与点G分别在线段BC与线段AD上时.
①求证：DG=2PC；
②求证：四边形PEFD是菱形；
(2)如图2，当点P与点G分别在线段BC与线段AD的延长线上时，请猜想四边形PEFD
是怎样的特殊四边形，并证明你的猜想.
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，平面直角坐标系中，△ABC的顶点坐标分别是A(－3，1)，B(－1，1)，
C(－2，2)，当直线y﹦－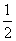
x+b与△ABC有公共点时，b的取值范围是（ ）
A．－1≤b≤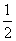 B．－1≤b≤1 C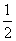．－≤b≤1 D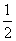．－≤b≤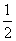
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
以下是根据南京市国民经济和社会发展统计公报中的相关数据，绘制统计图的一部分．
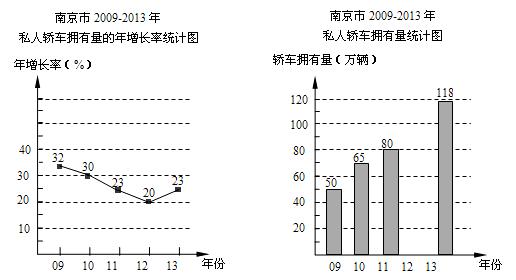
请根据以上信息解答下列问题：
（1）2012年南京市私人轿车拥有是多少万辆？
（2）补全条形统计图；
（3）经测定，汽车的碳排放量与汽车的排量大小有关．如驾驶排量1．6L的轿车，若一年行驶里程1万千米，则这一年，该轿车的碳排放量约为2．7吨．经调查，南京市某小区的300辆私人轿车，不同排量的数量统计如下表：
| 排量（L） | 小于1．6 | 1．6 | 1．8 | 大于1．8 |
| 数量（辆） | 30 | 150 | 62 | 58 |
请按照上述的统计数据，通过计算估计，2013年南京市仅排量为1．6L的私人轿车（假定每辆车平均一年行驶的路程都为1万千米）的碳排放总量约为多少万吨？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
∥
，直线
与
C．65° D．125°
如图，在等边
中，
为
边上一点，
为
边上
则