
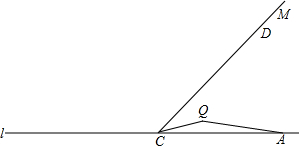
分析 (1)要分类讨论,当点Q在点C的左侧,当点Q在点C的右侧两种情况;
(2)因为QA=2QC,所以求2QD+QA的最小值就是求2QD+2QC的最小值.QD+QC≥CD,所以QD+QC最小值为CD=7,题中所求最小值为14.
解答 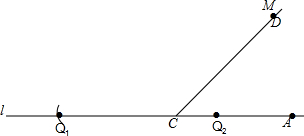 解:(1)①如图所示:点Q即为所求;
解:(1)①如图所示:点Q即为所求;
②(Ⅰ)当点Q在点C的左侧,
∵QA=2QC,
∴CQ=AC=6,
(Ⅱ)当点Q在点C的右侧,
∵QA=2QC,
∴CQ=$\frac{1}{3}$AC=2.
故答案为:6或2;
(2)∵QA=2QC,
∴2QD+QA=2QD+2QC,
∵QD+QC≥CD,
∴QD+QC的最小值=CD=7,
∴2QD+QA的最小值=14.
故答案为;14.
点评 本题考查了基本作图,线段和的最小值,特别是(1)要进行分类讨论.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
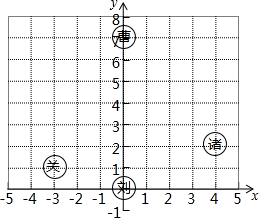 三国时期的一次战役中,曹军的位置在(0,7),蜀军的3支部队位置如图所示,诸葛亮安排关羽先向北然后向东移动刘备向北移动,张飞先向北再向西移动,从三面围击曹军.
三国时期的一次战役中,曹军的位置在(0,7),蜀军的3支部队位置如图所示,诸葛亮安排关羽先向北然后向东移动刘备向北移动,张飞先向北再向西移动,从三面围击曹军.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
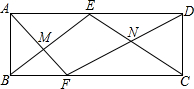 如图,矩形ABCD中,点E、F分别在边AD、BC上,AF、BE交于M,DF、CE交于N,且△AME的面积是4,△BMF的面积是2,△DCN的面积是3.则矩形EMFN的面积是2$\sqrt{2}$+3.
如图,矩形ABCD中,点E、F分别在边AD、BC上,AF、BE交于M,DF、CE交于N,且△AME的面积是4,△BMF的面积是2,△DCN的面积是3.则矩形EMFN的面积是2$\sqrt{2}$+3.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}{a=4}\\{b=1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{a=-4}\\{b=-1}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{a=-4}\\{b=1}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{a=4}\\{b=-1}\end{array}}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.
如图,?ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com